

分析 (1)易得点B、D的坐标,然后把这两个点的坐标代入抛物线的解析式,就可解决问题;
(2)△BCD的面积确定,要使四边形BCDM的面积S最大,只需△MBD的面积最大,过点M作MN⊥x轴于H,交BD于N,如图1.设点M的横坐标为t,运用割补法即可用t的代数式表示△MBD的面积,然后只需运用二次函数的最值性即可解决问题;
(3)显然∠POQ<90°,当∠OPQ=90°(①△OPQ≌△DHE,②若△QPO≌△DHE)时,过点PT⊥y轴于T,过点Q作QS⊥PT于S,如图2.设OT=n,只需用n的代数式表示出点Q的坐标,然后代入抛物线的解析式,再结合点Q在第二象限,就可解决问题;当∠OQP=90°(③若△PQO≌△DHE,④若△OQP≌△DHE)时,过点Q作QS⊥x轴于S,过点P作PT⊥QS于T,如图3.设PT=n,只需用n的代数式表示出点Q的坐标,然后代入抛物线的解析式,再结合点Q在第二象限,就可解决问题.
解答 解:(1)由题可得B(1,2),D(-3,0),
代入y=ax2+bx-$\frac{3}{2}$,得
$\left\{\begin{array}{l}{a+b-\frac{3}{2}=2}\\{9a-3b-\frac{3}{2}=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=\frac{5}{2}}\end{array}\right.$.
故二次函数的解析式为y=x2+$\frac{5}{2}$x-$\frac{3}{2}$;
(2)过点M作MN⊥x轴于H,交BD于N,如图1.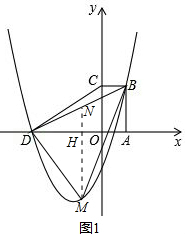
设直线BD的解析式为y=mx+n,
则有$\left\{\begin{array}{l}{m+n=2}\\{-3m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=\frac{3}{2}}\end{array}\right.$,
∴直线BD的解析式为y=$\frac{1}{2}$x+$\frac{3}{2}$.
设点M的横坐标为t,则有
yN=$\frac{1}{2}$t+$\frac{3}{2}$,yM=t2+$\frac{5}{2}$t-$\frac{3}{2}$,
∴MN=($\frac{1}{2}$t+$\frac{3}{2}$)-(t2+$\frac{5}{2}$t-$\frac{3}{2}$)=-t2-2t+3,
∴S△MBD=S△DMN+S△BMN=$\frac{1}{2}$MN•DH+$\frac{1}{2}$MN•AH
=$\frac{1}{2}$MN•AD=$\frac{1}{2}$(-t2-2t+3)×(1+3)
=-2(t2+2t-3)
=-2(t+1)2+8,
∵-2<0,
∴当t=-1时,S△MBD最大,最大值为8,
此时yM=(-1)2+$\frac{5}{2}$×(-1)-$\frac{3}{2}$=-3,
S△BCD=$\frac{1}{2}$×1×2=1,S=1+8=9,
∴S的最大值为9,此时点M的坐标为(-1,-3);
(3)存在P、Q使得以P、O、Q为顶点的三角形与△DEH全等,
此时点Q的坐标为(-$\frac{9+\sqrt{55}}{4}$,$\frac{11+4\sqrt{55}}{8}$)或(-$\frac{6+5\sqrt{2}}{4}$,$\frac{1+5\sqrt{2}}{8}$)或(-$\frac{9+\sqrt{65}}{4}$,$\frac{4+\sqrt{65}}{2}$).
提示:①若△OPQ≌△DHE,
过点PT⊥y轴于T,过点Q作QS⊥PT于S,如图2.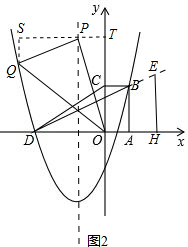
则有∠POQ=∠HDE,∠OPQ=∠DHE=90°,
则有$\frac{PQ}{PO}$=tan∠POQ=tan∠HOE=$\frac{AB}{AD}$=$\frac{1}{2}$.
易证△QSP∽△PTO,
从而可得$\frac{SQ}{TP}$=$\frac{SP}{TO}$=$\frac{PQ}{OP}$=$\frac{1}{2}$,
∴SQ=$\frac{1}{2}$TP,SP=$\frac{1}{2}$TO.
∵xP=-$\frac{\frac{5}{2}}{2×1}$=-$\frac{5}{4}$,
∴PT=$\frac{5}{4}$,SQ=$\frac{5}{8}$.
设OT=n,则有SP=$\frac{n}{2}$,
∴点Q的坐标为(-$\frac{5}{4}$-$\frac{n}{2}$,n-$\frac{5}{8}$),
代入y=x2+$\frac{5}{2}$x-$\frac{3}{2}$,解得n=$\frac{4±\sqrt{55}}{2}$.
∵点Q在第二象限,
∴-$\frac{5}{4}$-$\frac{n}{2}$<0且n-$\frac{5}{8}$>0,
∴n>$\frac{5}{8}$,
∴n=$\frac{4+\sqrt{55}}{2}$,
∴点Q的坐标为(-$\frac{9+\sqrt{55}}{4}$,$\frac{11+4\sqrt{55}}{8}$).
②若△QPO≌△DHE,
同①可得Q(-$\frac{5}{4}$-2n,n-$\frac{5}{2}$),n=$\frac{1±\sqrt{10}}{8}$.
∵点Q在第二象限,
∴-$\frac{5}{4}$-2n<0且n-$\frac{5}{2}$>0,
∴n>$\frac{5}{2}$,
∴n不存在;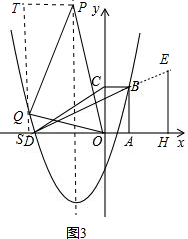
③若△PQO≌△DHE,
过点Q作QS⊥x轴于S,过点P作PT⊥QS于T,如图3.
易证△PTQ∽△QSO,
从而可得$\frac{PT}{QS}$=$\frac{PQ}{QO}$=$\frac{DH}{HE}$=2,
设PT=n,则有QS=$\frac{n}{2}$,
∴点Q的坐标为(-$\frac{5}{4}$-n,$\frac{n}{2}$),
代入抛物线y=x2+$\frac{5}{2}$x-$\frac{3}{2}$,
结合n>0可得n=$\frac{1+5\sqrt{2}}{4}$,
从而可得点Q的坐标为(-$\frac{6+5\sqrt{2}}{4}$,$\frac{1+5\sqrt{2}}{8}$).
④若△OQP≌△DHE,
同③可得点Q的坐标为(-$\frac{9+\sqrt{65}}{4}$,$\frac{4+\sqrt{65}}{2}$).
点评 本题主要考查了运用待定系数法求二次函数及一次函数的解析式、二次函数的最值性、抛物线上点的坐标特征、全等三角形的性质、相似三角形的判定与性质、解一元二次方程等知识,运用割补法及二次函数的最值性是解决第(2)小题的关键,运用分类讨论及构造K型相似是解决第(3)小题的关键.


科目:初中数学 来源: 题型:解答题
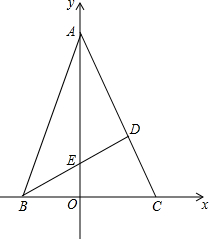 如图,在坐标系中,A(0,6),B(-2,0),C(3,0),∠BAC=45°,BD⊥AC,M(4,6),动点P从点M出发,沿x轴正方向,以每秒2个单位的长度运动t秒
如图,在坐标系中,A(0,6),B(-2,0),C(3,0),∠BAC=45°,BD⊥AC,M(4,6),动点P从点M出发,沿x轴正方向,以每秒2个单位的长度运动t秒查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
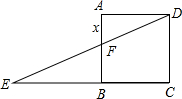 如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交A8于点F,AF=x(0.2≤x≤0.8),EC=y.则大致能反映y与x之闻函数关系的是y=$\frac{1}{x}$.
如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交A8于点F,AF=x(0.2≤x≤0.8),EC=y.则大致能反映y与x之闻函数关系的是y=$\frac{1}{x}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com