
����Ŀ����֪����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬ֱ��
Ϊ����ԭ�㣬ֱ��![]() �ֱ�
�ֱ�![]() �ᣬ
�ᣬ![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() �ڵ�һ���ޣ�����
�ڵ�һ���ޣ�����![]() ��
��![]() ���ı���
���ı���![]() �������Σ�
��������

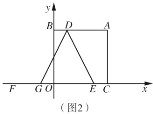
��1����ͼ1����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����ͼ2����![]() �ֱ���
�ֱ���![]() �ϣ���
�ϣ���![]() ����
����![]() ��ĶԳƵ�Ϊ��
��ĶԳƵ�Ϊ��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ������
������![]() ��
��![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ����ֱ��д���Ա���
֮��ĺ�����ϵʽ����ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
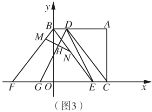
��3����ͼ3���ڣ�2���������£�����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��![]() �ϣ�����
�ϣ�����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ����2��
����2��![]() ����3��32
����3��32
��������
��1������C�����꣬�ٴ������ʽ�����k��
��2�����ݵ�E����y��ĶԳƵ�Ϊ��F��EG=2FG���Եó�OG��OE�Ĺ�ϵ���Ӷ��ó�GE��t�Ĺ�ϵ���ٸ��������������ʽ�������S��
��3����![]() ����
����![]() ��
��![]() ����
����![]() �У����ݹ��ɶ������n���ӳ�
�У����ݹ��ɶ������n���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ����
����![]() ���Ӷ�֤��
���Ӷ�֤��![]() ����
����![]() �У����ݹ��ɶ������m���Ӷ����S.
�У����ݹ��ɶ������m���Ӷ����S.
�⣺��1����![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��![]() ��
��
���ı���![]() �������Σ�
��������
��![]() ��
��
��![]() ��
��
�������ʽ��![]() ��
��
���![]() ��
��
��![]() ��
��
��2����ͼ������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
��![]() ��
��
���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��![]() ��
��
�ߵ�![]() ���
���![]() ����
����![]() ��Գƣ�
��Գƣ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
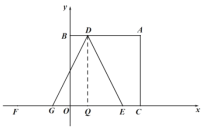
��3����ͼ����![]() ����
����![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
���![]() ��
��![]() ���ᣩ��
���ᣩ��
��![]() ��
��
�ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() �Ľ���Ϊ��
�Ľ���Ϊ��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�֡�![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
���![]() ���ᣩ��
���ᣩ��
��![]() ��
��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�����Ҫ����
��ģ�ͽ��ܣ�
��ͼ����C���߶�A��B��һ��E��F��ABͬ�࣬�ҡ�A����B����ECF��90��������ȥ��һ����K�������dz�ͼ��Ϊ��K����ͼ��
������̽����
����1����ͼ�٣���EC��FC����ACE�ա�BFC
����2����ͼ�٣���EC��FC����ACE����BFC�����ƱȲ�Ϊ1��
��ģ��Ӧ�ã�
Ӧ��1����ͼ�ڣ����ı���ABCD�У���ADC��90�㣬AD��1��CD��2��BC��2![]() ��AB��5����BD��
��AB��5����BD��
Ӧ��2����ͼ�ۣ���֪��ABC���ֱ���AB��ACΪ��������������ABGF��������ACDE��AH��BC������EF����AH�ķ����ӳ����ڵ�K��֤����KΪEF�е㣮
��1�������������1��֤�����̣�
��2����ֱ���Ӧ��1��Ӧ��2��������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
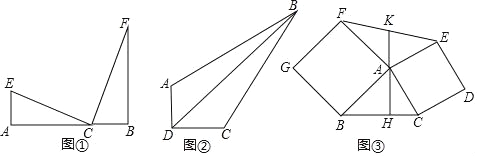
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ������C�ڰ�Բ�ϣ�����C�����߽�BA���ӳ����ڵ�D��CD=CB��CE��AB����Բ�ڵ�E��
��1�����D�Ķ�����
��2����֤���Ե�C��O��B��EΪ������ı��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
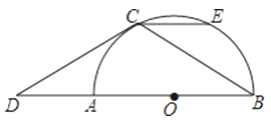
����Ŀ����ͼ��һ�κ���y=k1x+b��ͼ��A��0����2����B��1��0�����㣬�뷴��������![]() ��ͼ���ڵ�һ�����ڵĽ���ΪM������OBM�����Ϊ2��
��ͼ���ڵ�һ�����ڵĽ���ΪM������OBM�����Ϊ2��
��1����һ�κ����ͷ����������ı���ʽ��
��2����x�����Ƿ���ڵ�P��ʹAM��MP�������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ��ͼ�����ͬһ����ֱ��·�ϣ��״�ѧУȥͼ��ݣ��Ҵ�ͼ��ݻ�ѧУ���ס������˶����ٲ�����ͬʱ���������ȵ���Ŀ�ĵأ�����֮��ľ���![]() ���ף���ʱ��
���ף���ʱ��![]() �����ӣ�֮��ĺ�����ϵ��ͼ��ʾ������˵����ȷ���ǣ� ��
�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ������˵����ȷ���ǣ� ��
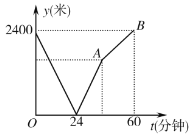
A.���ٶ���60��/����B.�ҵ��ٶ���80��/����
C.��![]() ������Ϊ
������Ϊ![]() D.�߶�
D.�߶�![]() ����ʾ�ĺ�������ʽΪ
����ʾ�ĺ�������ʽΪ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ǽ�ڷ�����ʱ�������ӵ���ǽ�ľ���ԼΪ���ӳ��ȵ�![]() �������ӱȽ��ȶ�����ͼ��ABΪһ����Ϊ6�����ӣ�
�������ӱȽ��ȶ�����ͼ��ABΪһ����Ϊ6�����ӣ�
��1���������ȶ��ڷ�ʱ�����Ķ����ܴﵽ5.7�ߵ�ǽͷ��
��2����ͼ2�������ӵ�������3![]() ��2���ף���ô���Ӷ��˽��»������ף�
��2���ף���ô���Ӷ��˽��»������ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����ڵ̱ߴ�������ͼ�٣��ӵ�AC���½�Ϊ30�㣬AC��![]() �ף�����AO����б����60�㣬�䳤Ϊ3�ף���AO�������OB�ļн�Ϊ60�㣬��ƯB��ӵ��¶�C֮��ľ���(��ͼ��)��
�ף�����AO����б����60�㣬�䳤Ϊ3�ף���AO�������OB�ļн�Ϊ60�㣬��ƯB��ӵ��¶�C֮��ľ���(��ͼ��)��
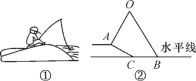
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ȱ���ABC�Ƶ�C˳ʱ����ת120���õ���EDC������AD��BD�������н��ۣ�
��AC=AD����BD��AC�����ı���ACED�����Σ�
������ȷ�ĸ����ǣ� ��

A��0 B��1 C��2 D��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com