【题目】如图，在
中，
，
，
，
，则
的长为（ ）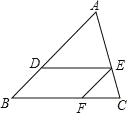
A.6B.8C.9D.10
【答案】D
【解析】
由DE∥BC可得出∠ADE＝∠B，结合∠ADE＝∠EFC可得出∠B＝∠EFC，进而可得出BD∥EF，结合DE∥BC可证出四边形BDEF为平行四边形，根据平行四边形的性质可得出DE＝BF，由DE∥BC可得出△ADE∽△ABC，根据相似三角形的性质可得出BC＝
DE，再根据CF＝BC﹣BF＝
DE＝6，即可求出DE的长度．
解：∵DE∥BC，
∴∠ADE＝∠B．
∵∠ADE＝∠EFC，
∴∠B＝∠EFC，
∴BD∥EF，
∵DE∥BF，
∴四边形BDEF为平行四边形，
∴DE＝BF．
∵DE∥BC，
∴△ADE∽△ABC，
∴
，
∴BC＝DE，
∴CF＝BC﹣BF＝DE＝6，
∴DE＝10．
故选：D．
科目：初中数学 来源： 题型：
【题目】某学校将开启“大阅读”活动，为了充实书吧藏书，学生会号召全年级学生捐书，得到各班的大力支持．同时，年级部分备课组的老师也购买藏书充实到年级书吧，其中数学组购买了甲、乙两种自然科学书籍若干本，用去699元；语文组购买了A、B两种文学书籍若干本，用去6138元，已知A、B的数量分别与甲、乙的数量相等，且甲种书与B种书的单价相同，乙种书与A种书的单价相同，若甲种书的单价比乙种书的单价多7元，则乙种书籍比甲种书籍多买了_____本．
．
查看答案和解析>>
科目：初中数学 来源： 题型：
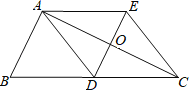
【题目】如图，已知△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，联结EC．
（1）求证：四边形ADCE是平行四边形；
（2）当∠BAC＝90°时，求证：四边形ADCE是菱形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在平面直角坐标系中，点
为坐标原点，直线
分别交
轴，
轴于点
，
，点
在第一象限，连接
，
，四边形
是正方形．
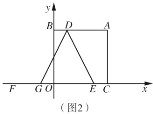
（1）如图1，求直线
的解析式；
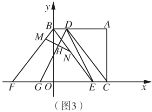
（2）如图2，点
分别在
上，点
关于轴的对称点为点
，点
在
上，且
，连接
，
，设点的横坐标为
，
的面积为
，求与之间的函数关系式，并直接写出自变量的取值范围；
（3）如图3，在（2）的条件下，连接
，
，
，点
在上，且
，点
在上，连接
交于点
，
，且
，若
，求的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
中，
，
，
．动点
、
均从顶点
同时出发，点在边
上运动，点在边
上运动．已知点的运动速度是
．当运动
停止时，由，，构成的三角形恰好与相似．
（1）试求点的运动速度；
（2）求出此时、两点间的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共50个，小颖做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是试验中的一组统计数据：
摸到球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的概率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
（1）请估计当
很大时，摸到白球的频率将会接近______；（精确到0.1）；
（2）假如随机摸一次，摸到白球的概率P（白球）＝______；
（3）试估算盒子里白色的球有多少个？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
