
Ζ÷Έω Θ®1Θ©ΗυΨίΕΞΒψΉχ±ξΙΪ ΫΘ§Ω…ΒΟ¥πΑΗΘΜ
Θ®2Θ©ΗυΨίΉ‘±δΝΩ”κΚ· ΐ÷ΒΒΡΕ‘”ΠΙΊœΒΘ§Ω…ΒΟPΒψΉχ±ξΘ§BΒψΉχ±ξΘ§ΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΘ§Ω…ΒΟ¥πΑΗΘΜ
Θ®2Θ©ΗυΨίΜΞœύ¥Ι÷±ΒΡΝΫ÷±œΏΒΡ±»άΐœΒ ΐΜΞΈΣΗΚΒΙ ΐΘ§Ω…ΒΟΙΊ”ΎmΒΡΖΫ≥ΧΘ§ΗυΨίΫβΖΫ≥ΧΘ§Ω…ΒΟmΒΡ÷ΒΗυΨίΉ‘±δΝΩ”κΚ· ΐ÷ΒΒΡΕ‘”ΠΙΊœΒΘ§Ω…ΒΟ¥πΑΗΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©”…ΕΞΒψΉχ±ξΘ§ΒΟ
$\left\{\begin{array}{l}{-\frac{b}{2a}=2}\\{\frac{4ac-{b}^{2}}{4a}=4}\end{array}\right.$Θ§
ΫβΒΟ$\left\{\begin{array}{l}{a=-1}\\{b=4}\end{array}\right.$ΘΜ
Θ®2Θ©Β±x=m ±Θ§y=-m2+4mΘ§Φ¥PΒψΉχ±ξΈΣΘ®mΘ§-m2+4mΘ©Θ§
Β±y=0 ±Θ§-x2+4x=0Θ§ΫβΒΟx=0Θ§x=4Φ¥BΒψΉχ±ξΈΣΘ®4Θ§0Θ©ΘΜ
S=$\frac{1}{2}$OB•yP=$\frac{1}{2}$ΓΝ4ΓΝΘ®-m2+4mΘ©=-2m2+8mΘΜ
Θ®3Θ©ΒψCΙΊ”ΎΒψBΒΡΕ‘≥ΤΒψCΓδΘ§¥φ‘Ύm÷ΒΘ§ ΙΓœAPCΓδ=90ΓψΘ§
…ηPΒψΉχ±ξΈΣΘ®mΘ§-m2+4mΘ©Θ§
»γΆΦΘΚ
ACΓΆy÷α”ΎCΒψΘ§ΒΟCΒψΉχ±ξΈΣΘ®0Θ§4Θ©Θ°
”…ΒψCΙΊ”ΎΒψBΒΡΕ‘≥ΤΒψCΓδΘ§ΒΟCΓδΒψΉχ±ξΈΣΘ®8Θ§-4Θ©Θ°
”…ΓœAPCΓδ=90ΓψΘ§ΒΟ
kAP•kCΓδP=-1Θ§
Φ¥$\frac{-{m}^{2}+4m-4}{m-2}$•$\frac{-{m}^{2}+4m+4}{m-8}$=-1Θ§
Μ·ΦρΘ§ΒΟm3-6m2+5m=0Θ°
ΫβΒΟm=0Θ®≤ΜΖϊΚœΧβ“βΘ§…αΘ©Θ§m=5Θ§m=1
Β±m=5 ±Θ§y=-m2+4m=-5Θ§Φ¥PΘ®5Θ§-5Θ©Θ§
Β±m=1 ±Θ§y=-m2+4m=3Θ§Φ¥PΘ®1Θ§3Θ©Θ°
Ήέ…œΥυ ωΘΚPΒψΉχ±ξΈΣΘ®1Θ§3Θ©ΜρΘ®5Θ§-5Θ©Θ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥΕΰ¥ΈΚ· ΐΉέΚœΧβΘ§άϊ”ΟΕΞΒψΉχ±ξ«σΚ· ΐΫβΈω ΫΘΜάϊ”ΟΉ‘±δΝΩ”κΚ· ΐ÷ΒΒΡΕ‘”ΠΙΊœΒΒΟ≥ωPΘ§BΒψΉχ±ξ «ΫβΧβΙΊΦϋΘΜάϊ”ΟΜΞœύ¥Ι÷±ΒΡΝΫ÷±œΏΒΡ±»άΐœΒ ΐΜΞΈΣΗΚΒΙ ΐΩ…ΒΟΙΊ”ΎmΒΡΖΫ≥Χ «ΫβΧβΙΊΦϋΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | -2axΘΨ-2b | BΘ° | 2axΘΨ2b | CΘ° | ax+2ΘΨb+2 | DΘ° | ax-2ΘΨb-2 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
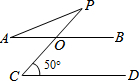 »γΆΦΘ§ABΓΈCDΘ§CPΫΜAB”ΎOΘ§AO=POΘ§»τΓœC=50ΓψΘ§‘ρΓœAΒΡΕ» ΐΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§ABΓΈCDΘ§CPΫΜAB”ΎOΘ§AO=POΘ§»τΓœC=50ΓψΘ§‘ρΓœAΒΡΕ» ΐΈΣΘ®ΓΓΓΓΘ©| AΘ° | 25Γψ | BΘ° | 35Γψ | CΘ° | 15Γψ | DΘ° | 50Γψ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
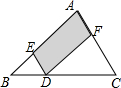 »γΆΦΘ§‘ΎΓςABC÷–Θ§Ε·ΒψD¥”ΒψB≥ωΖΔΘ§―ΊBCΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘»ΥΌ‘ΥΕ·ΒΫΒψCΘ®ΒψD≤Μ”κΒψBΓΔC÷ΊΚœΘ©Θ§‘ΥΕ· ±ΦδΈΣtΘ§ΙΐΒψDΉςDEΓΈACΘ§DEΓΈABΘ§Ζ÷±πΫΜAB”ΎΒψEΘ§ΫΜAC”ΎΒψFΘ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐS”κ ±Φδt÷°ΦδΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§‘ΎΓςABC÷–Θ§Ε·ΒψD¥”ΒψB≥ωΖΔΘ§―ΊBCΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘»ΥΌ‘ΥΕ·ΒΫΒψCΘ®ΒψD≤Μ”κΒψBΓΔC÷ΊΚœΘ©Θ§‘ΥΕ· ±ΦδΈΣtΘ§ΙΐΒψDΉςDEΓΈACΘ§DEΓΈABΘ§Ζ÷±πΫΜAB”ΎΒψEΘ§ΫΜAC”ΎΒψFΘ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐS”κ ±Φδt÷°ΦδΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣΘ®ΓΓΓΓΘ©| AΘ° | 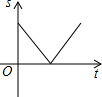 | BΘ° | 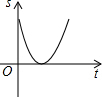 | CΘ° | 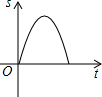 | DΘ° | 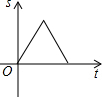 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com