
在平 面直角坐标系中,O为原点,直线y =-2x-1与y轴交于点A,与
面直角坐标系中,O为原点,直线y =-2x-1与y轴交于点A,与 直线y =-x交于点B, 点B关于
直线y =-x交于点B, 点B关于 原点的对称点为点C.
原点的对称点为点C.
(1)求过A,B,C三点的抛物线的解析式;
(2)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②若点P的横坐标为t(-1<t<1),当t为何值时,四边形PBQC面积最大,并说明理由.

解:(1)解方程组 得
得
∴点B的坐标为(-1,1).························ 1分
∵点C和点B关于原点对称,
∴点C的坐标为(1,-1).························ 2分
又∵点A是直线y=-2x-1与y轴的交点,
∴点A的坐标为(0,-1).························ 3分
设抛物线的解析式为y=ax2+bx+c,
∴ 解得
解得
∴抛物线的解析式为y=x2-x-1.······················ 5分
(2)①如图1,∵点P在抛物线上,
∴可设点P的坐标为(m,m2-m-1).
当四边形PBQC是菱形时,O为菱形的中心,
∴PQ⊥BC,即点P,Q在直线y = x上,
∴m = m2-m-1,····························· 7分
解得m = 1± .···························· 8分
.···························· 8分
∴点P的坐标为(1+ ,1+
,1+ )或(1-
)或(1- ,1-
,1- ).··········· 9分
).··········· 9分
 |  |
图1 图2
②方法一:
如图2,设点P的坐标为(t,t2 - t - 1).
过点P作PD∥y轴,交直线y = - x于点D,则D(t,- t).
分别过点B,C作BE⊥PD,CF⊥PD,垂足分别为点E,F.
∴PD = - t -( t2 - t -1) = - t2 + 1,BE + CF = 2,··········· 10分
∴S△PBC= PD·BE +
PD·BE + PD·CF
PD·CF
= PD·(BE + CF)
PD·(BE + CF)
= (- t2 + 1)×2
(- t2 + 1)×2
=- t2 + 1.··························· 12分
∴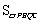 =-2t2+2.
=-2t2+2.
∴当t=0时,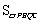 有最大值2. ···················· 13分
有最大值2. ···················· 13分
方法二:
如图3,过点B作y轴的平行线,过点C作x轴的平行线,两直线交于点D,连接PD.
∴S△PBC=S△BDC-S△PBD-S△PDC
= ×2×2-
×2×2- ×2(t+1)-
×2(t+1)- ×2(t2-t-1+1)
×2(t2-t-1+1)
=-t2+1.···························· 12分
∴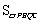 =-2t2+2.
=-2t2+2.
∴当t=0时,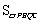 有最大值2. ···················· 13分
有最大值2. ···················· 13分
 | |||
 | |||
图3  图4
图4
方法三:如图4,过点P作PE⊥BC,垂足为E,作PF∥x轴交BC于点F.
∴PE=EF.
∵点P的坐标为(t,t2-t-1),
∴点F的坐标为(-t2+t+1,t2-t-1).
∴PF=-t2+t+1-t=-t2+1.
∴PE= (-t2+1).·························· 11分
(-t2+1).·························· 11分
∴S△PBC= BC·PE=
BC·PE= ×
× ×
× (-t2+1)
(-t2+1)
=-t2+1.···························· 12分
∴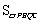 =-2t2+2.
=-2t2+2.
∴当t=0时,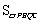 有最大值2.
有最大值2.


科目:初中数学 来源: 题型:
如图是函数 与函数
与函数 在第一象限内的图象,点
在第一象限内的图象,点 是
是 的图象上一动点,
的图象上一动点, 轴于点A,交
轴于点A,交 的
的 图象于点
图象于点 ,
,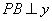 轴于点B,交
轴于点B,交 的图象于点
的图象于点 .
.
(1)求证:D是BP的中点;
(2)求出四边形ODPC的面积.
 |
…………………8分
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,直线y =-x+2与反比例函数 的图象有唯一公共点. 若直线
的图象有唯一公共点. 若直线 与反比例函数
与反比例函数 的图象有2个公共点,则b的取值范围是
的图象有2个公共点,则b的取值范围是
(A) b﹥2. (B) -2﹤b﹤2. (C) b﹥2或b﹤-2. (D) b﹤-2.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
“保护环境,人人有责”,为了了解某市的空气质量情况,某校环保兴趣小组,随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
请你根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)估计该市这一年(365天)空气质量达到“优 ”和“良”的总天数;
”和“良”的总天数;
(3)计算随机选取这一年内的某一天,空气质量是“优”的概率.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
生物学家发现了一种病毒的长度约为0.00000432毫米.数据0.00000432用科学记数法表示为 ( )
A. 0.432×10-5 B. 4.32×10-6 C. 4.32×10-7 D. 43.2×10-7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com