
【题目】如图,MN∥BC,BD⊥DC,∠1=∠2=60°. 
(1)AB与DE平行吗?请说明理由;
(2)若DC是∠NDE的平分线.
①试说明∠ABC=∠C;
②试说明BD是∠ABC的平分线.
(要求:第(1)小题要写出每一步的理由,第(2)小题的理由可省略不写.)
【答案】
(1)解:AB∥DE,理由如下:
∵MN∥BC(已知),
∴∠ABC=∠1=60°(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠ABC=∠2(等量代换),
∴AB∥DE(同位角相等,两直线平行)
(2)解:①∵MN∥BC,
∴∠1=∠ABC=60°,∠NDE+∠2=180°,
∴∠NDE=180°﹣∠2=180°﹣60°=120°,
∵DC是∠NDE的平分线,
∴∠EDC=∠NDC= ![]() ∠NDE=60°,
∠NDE=60°,
∵MN∥BC,
∴∠C=∠NDC=60°,
∴∠ABC=∠C;
②∠ADC=180°﹣∠NDC=180°﹣60°=120°,
∵BD⊥DC,
∴∠BDC=90°,
∴∠ADB=∠ADC﹣∠BDC=120°﹣90°=30°,
∵MN∥BC,
∴∠DBC=∠ADB=30°,
∴∠ABD=∠DBC= ![]() ∠ABC,
∠ABC,
∴BD是∠ABC的平分线
【解析】(1)根据平行线的性质得出∠ABC=∠1=60°,求出∠ABC=∠2,根据平行线的判定得出即可;(2)①根据平行线的性质得出∠1=∠ABC=60°,∠NDE+∠2=180°,求出∠EDC=∠NDC= ![]() ∠NDE=60°,根据平行线的性质得出∠C=∠NDC=60°,即可得出答案;②求出∠ADC=120°,求出∠ADB=30°,根据平行线的性质求出∠DBC=∠ADB=30°,即可得出答案.
∠NDE=60°,根据平行线的性质得出∠C=∠NDC=60°,即可得出答案;②求出∠ADC=120°,求出∠ADB=30°,根据平行线的性质求出∠DBC=∠ADB=30°,即可得出答案.
【考点精析】利用平行线的判定与性质对题目进行判断即可得到答案,需要熟知由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90![]() ,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED=
,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED= ![]() ;②
;②![]() ;③∠ADF=
;③∠ADF= ![]() ;④CE=DF.正确的是( )
;④CE=DF.正确的是( )
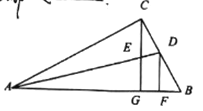
A. ①②④ B. ②③④ C. ①③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,

(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC的三条边a,b,c满足a2+2ab=c2+2bc,则△ABC的形状是( )
A. 直角三角形 B. 等腰直角三角形 C. 等边三角形 D. 等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年安徽全省生产总值比2017年增长8.02%,2017年比2016年增长8.5%.设安徽省这两年生产总值的年平均增长率为x,则所列方程正确的为( )
A. (1+x)2=8.02%×8.5%
B. (1+2x)2=8.02%×8.5%
C. (1+2x)2=(1+8.02%)×(1+8.5%)
D. (1+x)2=(1+8.02%)×(1+8.5%)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分△BFD剪去,得到△ABF和△EDF.

(1)判断△ABF与△EDF是否全等?并加以证明;
(2)把△ABF与△EDF不重合地拼在一起,可拼成特殊三角形和特殊四边形,将下列拼图(下图)按要求补充完整.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com