
 如图,AB是⊙O的直径,如果∠COA=∠DOB=60°,那么与线段OA相等的线段有AC,OC,CD,OD,BD,OB,与$\widehat{AC}$相等的弧有$\widehat{CD}$,$\widehat{BD}$.
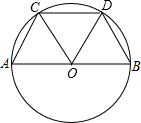
如图,AB是⊙O的直径,如果∠COA=∠DOB=60°,那么与线段OA相等的线段有AC,OC,CD,OD,BD,OB,与$\widehat{AC}$相等的弧有$\widehat{CD}$,$\widehat{BD}$. 分析 根据AB是⊙O的直径,于是得到∠AOC=∠COD=∠BOD=60°,则△AOC、△COD、△BOD均为等边三角形,由此得到结论.
解答 解:∵AB是⊙O的直径,∠COA=∠DOB=60°,
∴∠AOC=∠COD=∠BOD=60°;
又∵OA=OC=OD=OB,
∴△OAC、△OCD、△BOD是全等的等边三角形;
∴OA=AC=OC=CD=OD=BD=OB;
$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$,
故答案为:AC,OC,CD,OD,BD,OB,$\widehat{CD}$,$\widehat{BD}$,
点评 本题考查了圆周角、弦、弧的关系,能够发现△OAC、△OCD、△BOD是全等的等边三角形是解答此题的关键.


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6cm | B. | 12cm | C. | 2$\sqrt{3}$cm | D. | $\sqrt{6}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
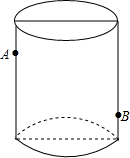 如图,有一个圆柱形杯子,底面周长为12cm,高为8cm,A点在内壁距杯口2cm处,在A点正对面的外壁距杯底2cm的B处有一只小虫,小虫要到A处饱餐一顿至少要走10cm.(杯子厚度忽略不计)
如图,有一个圆柱形杯子,底面周长为12cm,高为8cm,A点在内壁距杯口2cm处,在A点正对面的外壁距杯底2cm的B处有一只小虫,小虫要到A处饱餐一顿至少要走10cm.(杯子厚度忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
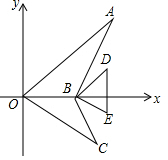 如图,将平面直角坐标系中图案的六个点的纵坐标保持不变,横坐标分别变成原来的2倍,连接各点所得图案与原图案相比( )
如图,将平面直角坐标系中图案的六个点的纵坐标保持不变,横坐标分别变成原来的2倍,连接各点所得图案与原图案相比( )| A. | 相同 | B. | 横向缩短一半 | C. | 横向拉长2倍 | D. | 纵向拉长2倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 小区绿化率(%) | 20 | 25 | 30 | 32 |
| 小区个数 | 2 | 4 | 3 | 1 |
| A. | 方差是13% | B. | 众数是25% | C. | 中位数是25% | D. | 平均数是26.2% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com