
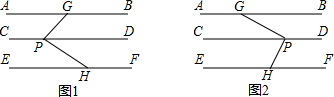
分析 由于AB∥CD是条件,因此理由是“已知”,由于∠DPH与∠EHP内错角,因此由CD∥EF推出∠DPH=∠EHP的理由是“两直线平行,内错角相等”,由∠GPD+∠DPH=∠GPH得到∠AGP+∠EHP=∠GPH,是将∠GPD换成∠AGP,将∠DPH换成∠EHP,因此理由是“等量代换”;
探究:只需运用平行线的性质就可解决问题;
应用:只需运用探究得到的结论就可解决问题.
解答 解:∵AB∥CD(已知)
∴∠AGP=∠GPD,
∵CD∥EF,
∴∠DPH=∠EHP(两直线平行,内错角相等)
∵∠GPD+∠DPH=∠GPH
∴∠AGP+∠EHP=∠GPH(等量代换).
故答案分别为:已知;两直线平行,内错角相等;等量代换.
探究:当点P在直线GH的右侧时,其他条件不变,如图2,∠AGP+∠EHP+∠GPH=360°.
理由如下:
∵AB∥CD,
∴∠AGP+∠GPC=180°,
∵CD∥EF,
∴∠CPH+∠EHP=180°,
∴∠AGP+∠GPC+∠CPH+∠EHP=360°,即∠AGP+∠GPH+∠EHP=360°;
应用:①当点P在直线GH的左侧时,则有∠AGP+∠EHP=∠GPH.
若∠GPH=70°,则∠AGP+∠EHP=70°;
②当点P在直线GH的右侧时,则有∠AGP+∠EHP+∠GPH=360°.
若∠GPH=70°,则∠AGP+∠EHP=360°-70°=290°.
综上所述:若∠GPH=70°,则∠AGP+∠EHP=70°或290°.
故答案为70°或290°.
点评 本题主要考查的平行线的性质、证明的格式等知识,运用分类讨论的思想是解决应用的关键.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
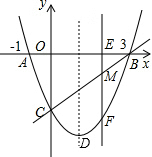 如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F
如图,抛物线与x轴交于点A(-1,0)、点B(3,0),交y轴于点C(0,-3),点M为线段BC上一动点,过点M作x轴的垂线,交x轴于点E,交抛物线于点F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
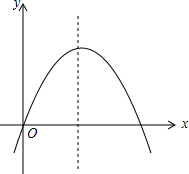 已知二次函数y=ax2+bx+c的图象如图所示,记m=|a-b+c|+|2a+b+c|,n=|a+b+c|+|2a-b-c|.抛物线与x轴的其中一个交点1<x2<3,试比较m与n的大小,并说明理由.
已知二次函数y=ax2+bx+c的图象如图所示,记m=|a-b+c|+|2a+b+c|,n=|a+b+c|+|2a-b-c|.抛物线与x轴的其中一个交点1<x2<3,试比较m与n的大小,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
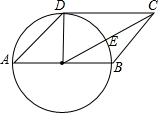 如图,在?ABCD中,AB=$\sqrt{2}$AD,以AB为直径的⊙O经过点D,连接OC交⊙O于点E.
如图,在?ABCD中,AB=$\sqrt{2}$AD,以AB为直径的⊙O经过点D,连接OC交⊙O于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
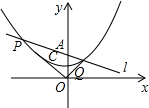 如图,O为坐标原点,直线l绕着点A(0,2)旋转,与经过点C(0,1)的抛物线y=$\frac{1}{4}$x2+h交于不同的点P,Q.求h的值.
如图,O为坐标原点,直线l绕着点A(0,2)旋转,与经过点C(0,1)的抛物线y=$\frac{1}{4}$x2+h交于不同的点P,Q.求h的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:单选题
某班数学兴趣小组10名同学的年龄情况如下表:
年龄(岁) | 12 | 13 | 14 | 15 |
人数 | 1 | 4 | 4 | 1 |
则这10名同学年龄的平均数和中位数分别是( )
A. 13.5,13.5 B. 13.5,13 C. 13,13.5 D. 13,14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com