
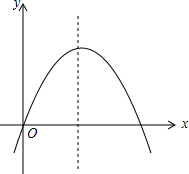
 已知二次函数y=ax2+bx+c的图象如图所示,记m=|a-b+c|+|2a+b+c|,n=|a+b+c|+|2a-b-c|.抛物线与x轴的其中一个交点1<x2<3,试比较m与n的大小,并说明理由.
已知二次函数y=ax2+bx+c的图象如图所示,记m=|a-b+c|+|2a+b+c|,n=|a+b+c|+|2a-b-c|.抛物线与x轴的其中一个交点1<x2<3,试比较m与n的大小,并说明理由. 分析 根据图象可得a<0,b>0,c=0,然后根据对称轴确定2a+b的符号,求m-n的值,判断差的符号即可.
解答 解:根据图象可得a<0,b>0,c=0.
则a-b<0,0<x=-$\frac{b}{2a}$<1,则-b>2a,即2a+b<0,2a-b<0,
当x=1是y=a+b+c=a+b>0,
则m-n=|a-b|+|2a+b|-(|a+b|+|2a-b|)
=b-a-(2a+b)-(a+b)+(2a-b)
=b-a-2a-b-a-b+2a-b
=-2a-2b=-2(a+b)<0,
则m<n.
点评 本题考查了二次函数的图象的性质以及比较代数式的方法,一般转化为判断差的符号,正确去掉绝对值符号是关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:填空题
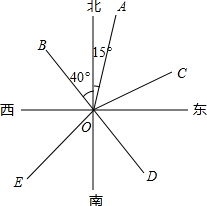 如图,OA的方向是北偏东15°,OB的方向是北偏西40°.
如图,OA的方向是北偏东15°,OB的方向是北偏西40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
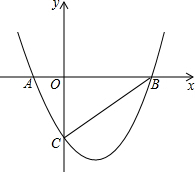 如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B,与y轴相交于点C,连接BC,在抛物线上找点D,连接CD,若∠BCD=90°,求点D的坐标.
如图,抛物线y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$与x轴相交于点A和点B,与y轴相交于点C,连接BC,在抛物线上找点D,连接CD,若∠BCD=90°,求点D的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-c | B. | (a-c)$\sqrt{b}$ | C. | $\sqrt{{a}^{2}b}$-$\sqrt{{c}^{2}b}$ | D. | a-c$\sqrt{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{3}}$ | B. | $\frac{3}{{\sqrt{3}}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com