
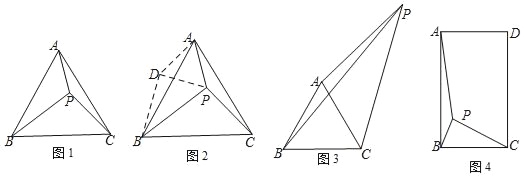
【题目】问题情境:如图1,在等边△ABC中,点P在△ABC内,且PA=3,PB=5,PC=4,求∠APC的度数?
小明在解决这个问题时,想到了以下思路:如图2,把△APC绕着点A顺时针旋转,使点C旋转到点B,得到△ADB,连结DP.
请你在小明的思路提示下,求出∠APC的度数.
思路应用:如图3,△ABC为等边三角形,点P在△ABC外,且PA=6,PC=8,∠APC=30°,求PB的长;
思路拓展:如图4,矩形ABCD中,AB=![]() BC,P为矩形ABCD内一点,PA:PB:PC=2
BC,P为矩形ABCD内一点,PA:PB:PC=2![]() :1:2,则∠APB= °.(直接填空)
:1:2,则∠APB= °.(直接填空)
【答案】见解析.
【解析】试题分析:问题情境,如图2中,只要证明△ADP为等边三角形,∠BDP=90°;
思路应用,如图,把△APC绕点A顺时针旋转,使点C与点B重合,得到△ADB,连接PD,只要证明△DAP是等边三角形,∠PDB=90°,即可解决问题;
思路拓展,如图4中,连接AC.作点P关于AB的对称点P1,点P关于BC的对称点P3,点P关于AC的对称点P2,连接AP1、P1B、P2A、P2C、P3B、P3C.只要证明△P1AP2是等边三角形,∠p2p1p3=90°,即可解决问题.
试题解析:问题情境,解:如图2中,
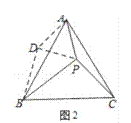
由旋转不变性可知,AD=AP=3,BD=PC=4,∠DAB=∠PAC,
∴∠DAP=∠BAC=60°,∴△ADP为等边三角形,
∴DP=PA=3,∠ADP=60°.
在△BDP中,DP=3,BD=4,PB=5,
∵32+42=52,∴∠BDP=90°,
∴∠ADB=∠ADP+∠BDP=60°+90°=150°,
∴∠APC=150°.
思路应用,解:如图,把△APC绕点A顺时针旋转,使点C与点B重合,得到△ADB,连接PD,
如图3中,∴△APC≌△ADB,
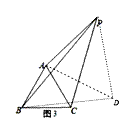
∴∠DAP=60°,AD=AP=6,DB=PC=8,∠PAC=∠DAB,∠ADB=∠APC=30°.
∴△DAP是等边三角形,
∴PD=6,∠ADP=60°,∴∠PDB=90°,∴PB2=PD2+DB2=62+82=100.
∴PB=10.
思路拓展,解:如图4中,连接AC.作点P关于AB的对称点P1,点P关于BC的对称点P3,点P关于AC的对称点P2,连接AP1、P1B、P2A、P2C、P3B、P3C.
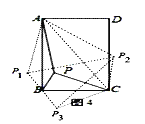
∵∠ABC=90°AB=![]() BC,∴tan∠BAC=
BC,∴tan∠BAC=![]() ,
,
∴∠BAC=30°,∠ACB=60°,根据对称性易知∠P1AP2=60°,P1A=P2A,∴△P1AP2是等边三角形,
∴∠AP1P2=60°,P1P2=PA=2![]() ,
,
根据对称性易知P1、B、P3共线,P1P3=2,△CP2P2的顶角为120°的等腰三角形,可得P2P3=2![]() ,
,
∴P1P22+p1p32=p2p32,∴∠p2p1p3=90°,∴∠APB=∠AP1B=90°+60°=150°.故答案为150.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,任意两点A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),规定运算:①A⊕B=(
),规定运算:①A⊕B=(![]() ,
, ![]() );②AB=
);②AB=![]() ;③当
;③当![]() 且
且![]() 时,A=B,有下列四个命题:(1)若A(1,2),B(2,﹣1),则A⊕B=(3,1),AB=0;
时,A=B,有下列四个命题:(1)若A(1,2),B(2,﹣1),则A⊕B=(3,1),AB=0;
(2)若A⊕B=B⊕C,则A=C;
(3)若AB=BC,则A=C;
(4)对任意点A、B、C,均有(A⊕B)⊕C=A⊕(B⊕C)成立,其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一蓄水池有漏水现象,如果用一台水泵向该水池注水,需用8小时才能将空水池注满,如果用同样的两台水泵向该水池注水,只需3.2小时就能将空池注满,如要求2小时内就将该水池注满,至少需要几台这样的水泵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=_______.
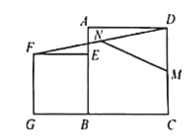
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是平行四边形ABCD的边BC、AD上的点,且BE=DF.
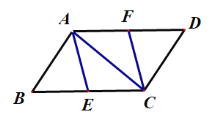
(1)求证:四边形AECF为平行四边形;
(2)若AE=BE,∠BAC=90°,判断四边形AECF的形状并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )

A.6 B.8 C.9 D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) | 水价(元/吨) |
第一级 20吨以下(含20吨) | 1.6 |
第二级 20吨﹣30吨(含30吨) | 2.4 |
第三级 30吨以上 | 3.2 |
例:某用户的月用水量为32吨,按三级计量应缴水费为:
1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴的水费为 元;
(2)如果乙用户缴的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多肉植物是指植物营养器官肥大的植物,又称肉质植物或多肉花卉,由于体积小、外形萌、色彩斑斓,茶几阳台摆放方便,近年来越来越受到广大养花爱好者的喜爱.多肉植物则被亲切地称为“肉肉”、“多肉君”.大学毕业生陈江河发现这个商机后,第一次果断购进甲乙两种多肉植物共500株.甲种多肉植物每株成本5元,售价10元;乙种多肉植物每株成本8元,售价10元.
(1)由于启动资金有限,第一次购进多肉植物的金额不得超过3400元,则甲种多肉植物至少购进多少株?
(2)多肉植物一经上市,十分抢手,陈江河决定第二次购进甲乙两种多肉植物,它们的进价不变.甲种多肉植物进货量在(1)的最少进货量的基础上增加了![]() ,售价也提高了
,售价也提高了![]() ;乙种多肉植物的售价和进货量不变,但是由于乙种多肉植物的耐热性不强,导致销售完之前它的成活率为
;乙种多肉植物的售价和进货量不变,但是由于乙种多肉植物的耐热性不强,导致销售完之前它的成活率为![]() .结果第二次共获利2700元.求m的值.
.结果第二次共获利2700元.求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com