
【题目】如图,已知矩形OABC中,OA=3,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
(k>0)与矩形两边AB、BC分别交于D、E,且BD=2AD
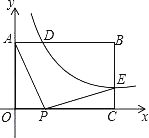
(1)求k的值和点E的坐标;
(2)点P是线段OC上的一个动点,是否存在点P,使∠APE=90°?若存在,求出此时点P的坐标,若不存在,请说明理由.
【答案】(1)k="4," E(4,1);(2)存在要求的点P,坐标为(1,0)或(3,0).
【解析】
试题(1)由矩形ABCD中,AB=4,BD=2AD,可得3AD=4,即可求得 AD的长,然后求得点D的坐标,即可求得K的值,继而求得点 E的坐标;(2)首先假设存在要求的点P坐标为(m,0),OP=m,CP=4-m,由∠APE=90,易证得△AOP∽△PCE,然后由相似三角形的对应边成比例,求得m的值,继而求得此时点P的坐标.
试题解析:(9分)(1)∵AB=4,BD=2AD,∴AB=AD+BD=AD+2AD=3AD=4,∴AD=![]() ,
,
又∵OA=3,所以D(![]() ,3),∵点D在双曲线
,3),∵点D在双曲线![]() 上,所以k=
上,所以k=![]() ×3=4.
×3=4.
∵四边形OABC为矩形,∴AB=OC=4,∴点E的横坐标为4.
把x=4代入![]() 中,得y=1,所以E(4,1).
中,得y=1,所以E(4,1).
(2)假设存在要求的点P坐标为(m,0),OP=m,CP=4-m.
∵∠APE=90,∴∠APO+∠EPC=90,又∵∠APO+∠OAP=90, ∴∠EPC=∠OAP,
又∵∠AOP=∠PCE=90,∴△AOP∽△PCE,∴![]() ,
,
∴![]() ,解得:m=1或m=3.
,解得:m=1或m=3.
所以,存在要求的点P,坐标为(1,0)或(3,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AB,交BC的延长线于D,交AC于点E,F是DE的中点,连接CF.
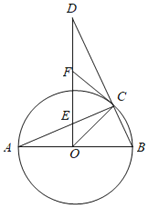
(1)求证:CF是⊙O的切线.
(2)若∠A=22.5°,求证:AC=DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为![]() 米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)
米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
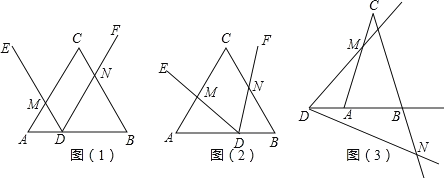
【题目】已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,设AM=x,BN=y,记△ADM的面积为S1,△BND的面积为S2.
(1)如图(1),当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,S1S2= ;
(2)在(1)的条件下,将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转如图(2)所示位置,
①求y与x的函数关系式;②求S1S2的值;
(3)当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α,如图(3),当点D在BA的延长线上运动时,设的AD=a,BD=b,直接写出S1S2的关系式(用含a、b和α的三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系内,正方形如图摆放,已知顶点 A(a,0),B(0,b) ,则顶点C的坐标为( )
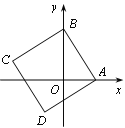
A.(-b,a b)B.(-b,b - a)C.(-a,b - a)D.(b,b -a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,∠BAC=120°,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
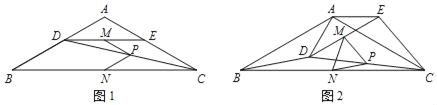
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,∠MPN的度数是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=8,请直接写出△PMN面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com