
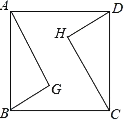
【题目】如图,在正方形ABCD中,AB=![]() ,AG=CH=3,BG=DH=2,则H、G两点之间的距离为_____.
,AG=CH=3,BG=DH=2,则H、G两点之间的距离为_____.
【答案】![]()
【解析】
延长BG交CH于点E,根据正方形的性质证明△ABG≌△CDH≌△BCE,可得GE=BE-BG=1、HE=CH-CE=1、∠HEG=90°,由勾股定理可得GH的长.
如图,延长BG交CH于点E,

∵AB=CD=![]() ,BG=DH=2,AG=CH=3,
,BG=DH=2,AG=CH=3,
∴AG2+BG2=AB2,
∴△ABG和△DCH是直角三角形,
在△ABG和△CDH中,
 ,
,
∴△ABG≌△CDH(SSS),
∴∠1=∠5,∠2=∠6,∠AGB=∠CHD=90°,
∴∠1+∠2=90°,∠5+∠6=90°,
又∵∠2+∠3=90°,∠4+∠5=90°,
∴∠1=∠3=∠5,∠2=∠4=∠6,
在△ABG和△BCE中,
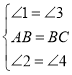 ,
,
∴△ABG≌△BCE(ASA),
∴BE=AG=3,CE=BG=2,∠BEC=∠AGB=90°,
∴GE=BE﹣BG=1,
同理可得HE=1,
在Rt△GHE中,GH=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(3,0),于y轴交于C.
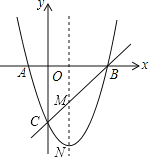
(1)求该抛物线的解析式;
(2)若M是抛物线的对称轴与直线BC的交点,N是抛物线的顶点,求MN的长;
(3)若点P是抛物线上点,当S△PAB=8时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
(1)收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=______,n=______.
(3)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 72 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=______,y=______.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有______人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF、DF
(1)求证:BF是⊙A的切线.
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD,等腰直角三角板的直角顶点落在正方形的顶点D处,使三角板绕点D旋转.
(1)当三角板旋转到图1的位置时,猜想CE与AF的数量关系,并加以证明;
(2)在(1)的条件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度数;
:3,求∠AED的度数;
(3)若BC= 4,点M是边AB的中点,连结DM,DM与AC交于点O,当三角板的一边DF与边DM重合时(如图2),若OF=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
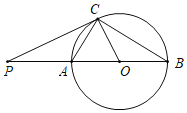
【题目】如图,已知AB是⊙O的直径,AC是弦,点P是BA延长线上一点,连接PC、BC,∠PCA=∠B.
(1)求证:PC是⊙O的切线;
(2)若PC=4,PA=2,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察与思考:阅读下列材料,并解决后面的问题.
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图1),则sinB=![]() ,sinC=
,sinC=![]() ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() .同理有:
.同理有:![]() ,
,![]() ,所以
,所以![]() =
=![]() ,即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.
,即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.
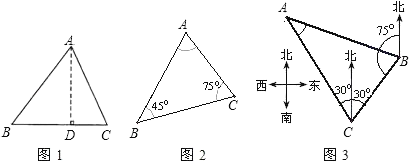
(1)如图2,△ABC中,∠B=45°,∠C=75°,BC=60,则∠A=_____;AC=_____;
(2)如图3,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图3),求此时货轮距灯塔A的距离AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
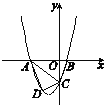
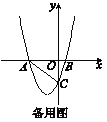
【题目】已知:如图16,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李珊一家准备假期游览华山(H)、秦始皇兵马俑(T)、大雁塔(G)三个景区,他用摸牌的方式确定游览顺序:如图,将代表三个景区的图片贴在背面完全相同的三张卡片上,将三张卡片背面向上洗匀后摸出一张(不再放回)作为最先游览的景区,再从剩下的两张卡片中摸出一张,作为游览的第二个景区,余下的一张代表最后游览的景区,比如:他先摸出T,再摸出G,则表示游览顺序为“T﹣G﹣H”,即“秦始皇兵马俑﹣大雁塔﹣华山”.
(1)求李珊一家最先游览的景区是大雁塔的概率;
(2)请用画树状图或列表的方法表示出所有可能的游览顺序,并求出李珊一家恰好按:“大雁塔﹣华山﹣秦始皇兵马俑”顺序游览的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com