
【题目】如图,射线![]() 表示一艘轮船的航行路线,从
表示一艘轮船的航行路线,从![]() 到
到![]() 的走向为南偏东30°,在
的走向为南偏东30°,在![]() 的南偏东60°方向上有一点
的南偏东60°方向上有一点![]() ,
,![]() 处到
处到![]() 处的距离为200海里.
处的距离为200海里.
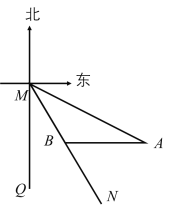
(1)求点![]() 到航线
到航线![]() 的距离.
的距离.
(2)在航线![]() 上有一点
上有一点![]() .且
.且![]() ,若轮船沿的速度为50海里/时,求轮船从
,若轮船沿的速度为50海里/时,求轮船从![]() 处到
处到![]() 处所用时间为多少小时.(参考数据:
处所用时间为多少小时.(参考数据:![]() )
)
【答案】(1)100海里(2)约为1.956小时
【解析】
(1)过A作AH⊥MN于H.由方向角的定义可知∠QMB=30°,∠QMA=60°,那么∠NMA=∠QMA-∠QMB=30°.解直角△AMH中,得出AH=![]() AM,问题得解;
AM,问题得解;
(2)先根据直角三角形两锐角互余求出∠HAM=60°,由∠MAB=15°,得出∠HAB=∠HAM-∠MAB=45°,那么△AHB是等腰直角三角形,求出BH=AH距离,然后根据时间=路程÷速度即可求解.
解:(1)如图,过![]() 作
作![]() 于
于![]() .
.
∵![]() ,
,
∴![]()
在直角![]() 中,
中,
∵![]() ,
,![]() ,
,![]() 海里,
海里,
∴![]() 海里.
海里.
答:点![]() 到航线
到航线![]() 的距离为100海里.
的距离为100海里.
(2)在直角![]() 中,
中,![]() ,
,
由(1)可知![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴轮船从![]() 处到
处到![]() 处所用时间约为
处所用时间约为![]() 小时.
小时.
答:轮船从![]() 处到
处到![]() 处所用时间约为1.956小时.
处所用时间约为1.956小时.


科目:初中数学 来源: 题型:
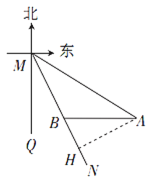
【题目】如图,隧道的截面由抛物线和长方形OABC构成,长方形的长OA是12m,宽OC是4m.按照图中所示的平面直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
x2+bx+c表示.在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m.那么两排灯的水平距离最小是( )
A.2mB.4mC.![]() mD.
mD.![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
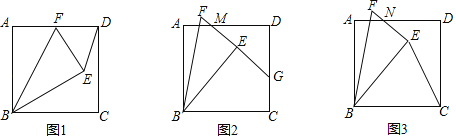
【题目】如图,正方形ABCD的边长为6,把一个含30°的直角三角形BEF放在正方形上,其中∠FBE=30°,∠BEF=90°,BE=BC,绕B点转动△FBE,在旋转过程中,
(1)如图1,当F点落在边AD上时,求∠EDC的度数;
(2)如图2,设EF与边AD交于点M,FE的延长线交DC于G,当AM=2时,求EG的长;
(3)如图3,设EF与边AD交于点N,当tan∠ECD=![]() 时,求△NED的面积.
时,求△NED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-![]() x+2与x 轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=
x+2与x 轴交于C,与y轴交于D,以CD为边作矩形CDAB,点A在x轴上,双曲线y=![]() (k<0)经过点B与直线CD交于E,EM⊥x轴于M,则SBEMC=______
(k<0)经过点B与直线CD交于E,EM⊥x轴于M,则SBEMC=______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平行四边形![]() 中,
中,![]() 于
于![]() ,
,![]() 平分
平分![]() 交线段
交线段![]() 于
于![]() .
.
(1)如果![]() ,求证:
,求证:![]() ;
;
(2)一般的情况下,如果![]() ,试探究线段
,试探究线段![]() 、
、![]() 与
与![]() 之间的所满足的等量关系(其中
之间的所满足的等量关系(其中![]() ,
,![]() 是已知数).
是已知数).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com