
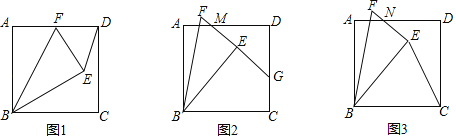
【题目】如图,正方形ABCD的边长为6,把一个含30°的直角三角形BEF放在正方形上,其中∠FBE=30°,∠BEF=90°,BE=BC,绕B点转动△FBE,在旋转过程中,
(1)如图1,当F点落在边AD上时,求∠EDC的度数;
(2)如图2,设EF与边AD交于点M,FE的延长线交DC于G,当AM=2时,求EG的长;
(3)如图3,设EF与边AD交于点N,当tan∠ECD=![]() 时,求△NED的面积.
时,求△NED的面积.
【答案】(1)15°;(2)3;(3)![]()
【解析】
(1)作EH⊥BC于H,EM⊥CD于M.则四边形EMCH是矩形.想办法证明EM垂直平分CD即可解决问题;
(2)连接BM、BG.由△BMA≌△BME,△BGE≌△BGC,推出AM=EM=2,EG=CG,设EG=CG=x,则DG=6﹣x.在Rt△DMG中,根据MG2=DG2+DM2,列出方程即可解决问题;
(3)连接BN,延长FE交CD于G,连接BG.只要证明∠ECD=∠GCB,推出tan∠GBC=tan∠ECD=![]() ,推出CG=2,由CD=6,可得CG=DG=2,设AN=EN=y,则DN=6﹣y,在Rt△DNG中,利用勾股定理求出y即可解决问题.
,推出CG=2,由CD=6,可得CG=DG=2,设AN=EN=y,则DN=6﹣y,在Rt△DNG中,利用勾股定理求出y即可解决问题.
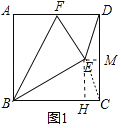
解:(1)如图1中,作EH⊥BC于H,EM⊥CD于M.则四边形EMCH是矩形.
∵四边形ABCD是正方形,
∴BA=BC=CD,∠ABC=∠BCD=90°,
∵BC=BE,
∴AB=BE=CD,
在Rt△BFA和Rt△BFE中,![]() ,
,
∴Rt△BFA≌△Rt△BFE(HL),
∴∠ABF=∠EBF=30°,
∵∠ABC=90°,
∴∠EBC=30°,
∴EH=MC=![]() BE=
BE=![]() CD,
CD,
∴DM=CM,
∵EM⊥CD,
∴ED=EC,
∵∠BCE=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴∠EDC=∠ECD=15°.
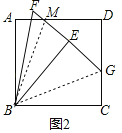
(2)如图2中,连接BM、BG.
∵AM=2,
∴DM=AD﹣AM=4,
由(1)可知△BMA≌△BME,△BGE≌△BGC,
∴AM=EM=2,EG=CG,
设EG=CG=x,则DG=6﹣x.
在Rt△DMG中,MG2=DG2+DM2,
∴(2+x)2=(6﹣x)2+42,
∴x=3,
∴EG=3.
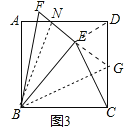
(3)如图3中,连接BN,延长FE交CD于G,连接BG.
AN=NE,EG=CG,
∵BE=BC,
∴BG垂直平分CE,
∴∠ECG+∠BCG=90°,∵∠GBC+∠ECB=90°,
∴∠ECD=∠GCB,
∴tan∠GBC=tan∠ECD=![]() ,
,
∴![]() =
=![]() ,
,
∴CG=![]() BC=2,
BC=2,
∵CD=6,
∴DG=CD﹣CG=4,设AN=EN=y,则DN=6﹣y,
在Rt△DNG中,(6﹣y)2+42=(2+y)2,
解得:y=3,
∴AN=NE=3,DN=3,NG=5,
∴S△NED=![]() S△DNG=
S△DNG=![]() ×
×![]() ×3×4=
×3×4=![]() .
.


科目:初中数学 来源: 题型:
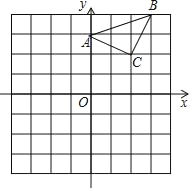
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四张正面分别印有![]() 和
和![]() 四种图案,并且其余完全相同的卡片,现将印有图案的一面朝下,并打乱摆放顺序,请用列表或画树状图的方法解决下列问题:
四种图案,并且其余完全相同的卡片,现将印有图案的一面朝下,并打乱摆放顺序,请用列表或画树状图的方法解决下列问题:

(1)现从中随机抽取一张,记下图案后放回,再从中随机抽取一张卡片,求两次摸到的卡片上印有图案都是轴对称图形的概率;
(2)现从中随机抽取-张,记下图案后不放回,再从中随机抽取一张卡片,求两次摸到的卡片上印有图案都是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
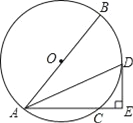
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明登陆泰微课学习页面后,发现推荐的数学微课有四个,其中有两个等级为A,另外两个等级为B,如果小明点击微课学习是随机的,且每个微课只点击学习一次.
(1)求小明第一次点击学习的微课等级为A的概率;
(2)如果小明第一次点击的微课等级为A,小明继续点击学习两次,利用树状图或表格求三次点击学习中有两个等级为A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
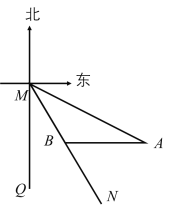
【题目】如图,射线![]() 表示一艘轮船的航行路线,从
表示一艘轮船的航行路线,从![]() 到
到![]() 的走向为南偏东30°,在
的走向为南偏东30°,在![]() 的南偏东60°方向上有一点
的南偏东60°方向上有一点![]() ,
,![]() 处到
处到![]() 处的距离为200海里.
处的距离为200海里.
(1)求点![]() 到航线
到航线![]() 的距离.
的距离.
(2)在航线![]() 上有一点
上有一点![]() .且
.且![]() ,若轮船沿的速度为50海里/时,求轮船从
,若轮船沿的速度为50海里/时,求轮船从![]() 处到
处到![]() 处所用时间为多少小时.(参考数据:
处所用时间为多少小时.(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月6日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不少于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示:
时间x(天) | 1≤x≤7 | 8≤x≤14 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 |
销量(斤) | 80﹣3x | 120﹣x |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 |
已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x≤14)之间的函数关系式,并求出第几天时销售利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com