
【题目】正方形ABCD的边长为8,点P是边AD的中点,点E是正方形ABCD的边上一点,若![]() 是等腰三角形,则腰长为______.
是等腰三角形,则腰长为______.
【答案】5或![]() 或
或![]()
【解析】
分情况讨论:![]() 当PB为腰时,若P为顶点,则E点和C点重合,求出PB长度即可;若B为顶点,则E点为CD中点;
当PB为腰时,若P为顶点,则E点和C点重合,求出PB长度即可;若B为顶点,则E点为CD中点;![]() 当PB为底时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
当PB为底时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
①由题意得出![]() ,证明
,证明![]() ∽
∽![]() ,得出比例式
,得出比例式![]() ,即可求出BE;②设
,即可求出BE;②设![]() ,则
,则![]() ,根据勾股定理得出方程求出CE,再由勾股定理求出BE即可.
,根据勾股定理得出方程求出CE,再由勾股定理求出BE即可.
分情况讨论:![]() 当PB为腰时,若P为顶点,则E点与C点重合,如图1所示:
当PB为腰时,若P为顶点,则E点与C点重合,如图1所示: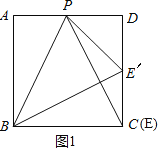
![]() 四边形ABCD是正方形,
四边形ABCD是正方形,![]() ,
,![]() ,
,![]() 是AD的中点,
是AD的中点,![]() ,
,
根据勾股定理得:![]() ;
;
若B为顶点,则根据![]() 得,
得,![]() 为CD中点,此时腰长
为CD中点,此时腰长![]() ;
;![]() 当PB为底边时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
当PB为底边时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
当E在AB上时,如图2所示:
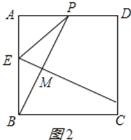
则![]() ,
,![]() ,
,![]() ,
,![]() ∽
∽![]() ,
,![]() ,即
,即![]() ,
,![]() ;
;
②当E在CD上时,如图3所示:
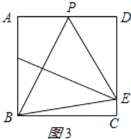
设![]() ,则
,则![]() ,
,
根据勾股定理得:![]() ,
,![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,![]() ;
;
综上所述:腰长为:![]() ,或5,或
,或5,或![]() ;
;
故答案为:![]() ,或5,或
,或5,或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中顶点为点M的抛物线是由抛物线![]() 向右平移1个单位得到的,它与y轴负半轴交于点A,点B在抛物线上,且横坐标为3.
向右平移1个单位得到的,它与y轴负半轴交于点A,点B在抛物线上,且横坐标为3.
![]() 写出以M为顶点的抛物线解析式.
写出以M为顶点的抛物线解析式.
![]() 连接AB,AM,BM,求
连接AB,AM,BM,求![]() ;
;
![]() 点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为
点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为![]() ,当
,当![]() 时,求点P坐标.
时,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() ,求代数式
,求代数式![]() 的值.
的值.
(2)2018年6月武侯区某学校开展了主题为“阳光下成长,妙笔绘武侯”学生绘画书法作品比赛,要求参赛学生每人交一件作品. 现将从中挑选的40件参赛作品的成绩(单位:分)统计如下:
等级 | 成绩(用 | 频数 | 频率 |
|
|
| 0.2 |
|
| 20 |
|
|
| 12 | 0.3 |
请根据上表提供的信息,解答下列问题:
①表中![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
②将本次获得![]() 等级的参赛作品依次用标签
等级的参赛作品依次用标签![]() 表示. 学校决定从中选取两件作品进行全校展示,
表示. 学校决定从中选取两件作品进行全校展示,![]() 所代表的作品必须参展,另一件作品从
所代表的作品必须参展,另一件作品从![]() 等级余下的作品中抽取,求展示作品刚好是
等级余下的作品中抽取,求展示作品刚好是![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:如图1,D是等边三角形ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边三角形DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图2,当动点D运动到等边三角形ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?如果成立,请证明;如果不成立,是否有新的结论?如果有新的结论,直接写出新的结论,不需证明.
(3)深入探究:①如图3,当动点D在等边三角形ABC的边BA上运动时(点D与点B不重合),连接DC,以DC为边在其上方、下方分别作等边三角形DCF和等边三角形DCF',连接AF,BF′.探究AF,BF′与AB有何数量关系?并证明你发现的结论。
②如图4,当动点D在等边三角形ABC的边BA的延长线上运动时,其他作法与图3相同,①中的结论是否仍然成立?如果成立,请证明;如果不成立,是否有新的结论?如果有新的结论,直接写出新的结论,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
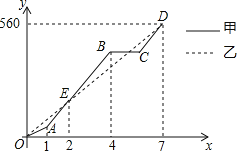
【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程![]() ,
,![]() 与时间
与时间![]() 之间的函数关系的图象
之间的函数关系的图象![]() 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题:
![]() 图中E点的坐标是______,题中
图中E点的坐标是______,题中![]() ______
______![]() ,甲在途中休息______h;
,甲在途中休息______h;
![]() 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围;
![]() 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.

请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为 度,该班共有学生 人, 训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
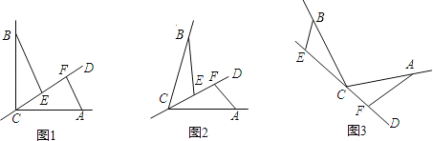
【题目】CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE_____CF;EF_____|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件_____,使①中的两个结论仍然成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并给出理由。.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清明节假期的某天,小强骑车从家出发前往革命烈士陵园扫墓,匀速行驶一段时间后,因车子出现问题,途中耽搁了一段时间,车子修好后,以更快的速度匀速前行,到达烈士陵园扫完墓后匀速骑车回家.其中![]() 表示小强从家出发后的时间,
表示小强从家出发后的时间,![]() 表示小强离家的距离,下面能反映变量
表示小强离家的距离,下面能反映变量![]() 与
与![]() 之间关系的大致图象是( )
之间关系的大致图象是( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com