
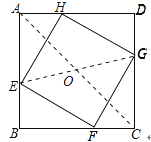
【题目】如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形
(2)判断直线EG是否经过一个定点,并说明理由
(3)求四边形EFGH面积的最小值.
【答案】
(1)
证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG,
在△AEH、△BFE、△CGF和△DHG中,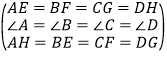 ,
,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形
(2)
解:直线EG经过一个定点,这个定点为正方形的中心(AC、BD的交点);理由如下:
连接AC、EG,交点为O;如图所示:
∵四边形ABCD是正方形,
∴AB∥CD,
∴∠OAE=∠OCG,
在△AOE和△COG中,
∠OAE=∠OCG
∠AOE=∠COG
AE=CG
∴△AOE≌△COG(AAS),
∴OA=OC,即O为AC的中点,
∵正方形的对角线互相平分,
∴O为对角线AC、BD的交点,即O为正方形的中心
(3)
解:设四边形EFGH面积为S,设BE=xcm,则BF=(8﹣x)cm,
根据勾股定理得:EF2=BE2+BF2=x2+(8﹣x)2,
∴S=x2+(8﹣x)2=2(x﹣4)2+32,
∵2>0,
∴S有最小值,
当x=4时,S的最小值=32,
∴四边形EFGH面积的最小值为32cm2.

【解析】(1)由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出结论;
(2)连接AC、EG,交点为O;先证明△AOE≌△COG,得出OA=OC,证出O为对角线AC、BD的交点,即O为正方形的中心;
(3)设四边形EFGH面积为S,BE=xcm,则BF=(8﹣x)cm,由勾股定理得出S=x2+(8﹣x)2=2(x﹣4)2+32,S是x的二次函数,容易得出四边形EFGH面积的最小值.


科目:初中数学 来源: 题型:
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y= ![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( ) 
A.![]()
B.![]()
C.![]()
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=mx+n与双曲线y=![]() 相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C
相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C
(1)求m,n的值
(2)若点D与点C关于x轴对称,求△ABD的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF.
(1)直接写出点F的坐标:
(2)求线段OB的长及图中阴影部分的面积:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一次函数y=kx+b的图象与二次函数y=x2的图象相交于A,B两点,点A,B的横坐标分别为m,n(m<0,n>0).
(1)当m=﹣1,n=4时,k= ,b= ;
当m=﹣2,n=3时,k= ,b= ;
(2)根据(1)中的结果,用含m,n的代数式分别表示k与b,并证明你的结论;
(3)利用(2)中的结论,解答下列问题:
如图②,直线AB与x轴,y轴分别交于点C,D,点A关于y轴的对称点为点E,连接AO,OE,ED.
①当m=﹣3,n>3时,求 ![]() 的值(用含n的代数式表示);
的值(用含n的代数式表示);
②当四边形AOED为菱形时,m与n满足的关系式为_____ ;
当四边形AOED为正方形时,m= , n= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com