
【题目】图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
科目:初中数学 来源: 题型:
【题目】一测量爱好者,在海边测量位于正东方向的小岛高度AC,如图所示,他先在点B测得山顶点A的仰角为30°,然后向正东方向前行62米,到达D点,在测得山顶点A的仰角为60°(B、C、D三点在同一水平面上,且测量仪的高度忽略不计).求小岛高度AC(结果精确的1米,参考数值: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2﹣2mx+m2+m﹣1(m是常数)的顶点为P,直线l:y=x﹣1
(1)求证:点P在直线l上。
(2)当m=﹣3时,抛物线与x轴交于A,B两点,与y轴交于点C,与直线l的另一个交点为Q,M是x轴下方抛物线上的一点,∠ACM=∠PAQ(如图),求点M的坐标
(3)若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形,请直接写出所有符合条件的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形
(2)判断直线EG是否经过一个定点,并说明理由
(3)求四边形EFGH面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,半径为R,圆心角为n°的扇形面积是S扇形=![]() ,由弧长l=
,由弧长l=![]() ,得S扇形=
,得S扇形=![]() =
=![]()
![]() R=
R=![]() lR.通过观察,我们发现S扇形=
lR.通过观察,我们发现S扇形=![]() lR类似于S三角形=
lR类似于S三角形=![]() ×底×高.
×底×高.
类比扇形,我们探索扇环(如图②,两个同心圆围成的圆环被扇形截得的一部分交作扇环)的面积公式及其应用.
(1)设扇环的面积为S扇环 , ![]() 的长为l1 ,
的长为l1 , ![]() 的长为l2 , 线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形=
的长为l2 , 线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形=![]() ×(上底+下底)×高,用含l1 , l2 , h的代数式表示S扇环 , 并证明;
×(上底+下底)×高,用含l1 , l2 , h的代数式表示S扇环 , 并证明;
(2)用一段长为40m的篱笆围成一个如图②所示的扇环形花园,线段AD的长h为多少时,花园的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,已知AD>AB.在边AD上取点E,使AE=AB,连结CE,过点E作EF⊥CE,与边AB或其延长线交于点F.
猜想:如图①,当点F在边AB上时,线段AF与DE的大小关系为______.
探究:如图②,当点F在边AB的延长线上时,EF与边BC交于点G.判断线段AF与DE的大小关系,并加以证明.
应用:如图②,若AB=2,AD=5,利用探究得到的结论,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是“东方之星”救援打捞现场图,小红据此构造出一个如图2所示的数学模型,已知:A、B、D三点在同一水平线上,CD⊥AD,∠A=30°,∠CBD=75°,AB=60m.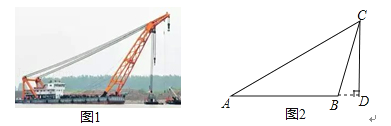
(1)求点B到AC的距离.
(2)求线段CD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com