

分析 (1)根据勾股定理求出AC的长度,根据平移得到PQ∥AB,
(2)由△CPM∽△CBA,得到$\frac{CP}{CB}$=$\frac{PM}{AB}$=$\frac{CM}{AC}$,则表示出PM=$\frac{12}{5}$-$\frac{3}{5}$t,CM=$\frac{16-4t}{5}$,即可;
(3)根据面积关系 S△QDC:S四边形ABQP=1:4建立方程,求出时间;
(4)由△DQP∽△PMQ,得到$\frac{PD}{PQ}$=$\frac{PQ}{MQ}$,从而得出PM2+MQ2=MD×MQ 即可.
解答 解:(1)在Rt△ABC中,AC=$\sqrt{{BC}^{2}{-AB}^{2}}$=4
∵PQ∥AB
∴$\frac{PC}{AC}$=$\frac{CQ}{CB}$,
∴$\frac{4-t}{4}$=$\frac{t}{5}$,
∴t=$\frac{20}{9}$,
(2)过点P作PM⊥BC于M,
∵△CPM∽△CBA,
∴$\frac{CP}{CB}$=$\frac{PM}{AB}$=$\frac{CM}{AC}$,
∴,$\frac{4-t}{5}$=$\frac{PM}{3}$=$\frac{CM}{4}$,
∴PM=$\frac{12}{5}$-$\frac{3}{5}$t,CM=$\frac{16-4t}{5}$,
∴S△PQC=$\frac{1}{2}$QC×$\frac{1}{2}$t($\frac{12}{5}$-$\frac{3}{5}$t)=$\frac{6}{5}$t-$\frac{3}{10}$t2,
∴y=-$\frac{3}{10}$t2+$\frac{6}{5}$t(0<t<4)
(3)∵PD∥BC,
∴S△QPC=S△QDC
∵S△QDC:S四边形ABQP=1:4
∴S△QPC:S四边形ABQP=1:4
∴S△QPC:S△ABC=1:5
∴$\frac{\frac{6}{5}t-{\frac{3}{10}t}^{2}}{6}=\frac{1}{5}$,
∴t1=t2=2
(4)t=$\frac{3}{2}$时,PQ⊥MQ,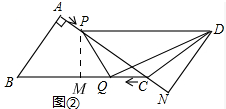
∵PQ⊥DQ,
∴∠DMQ=∠PMQ,=90°,
∵DP∥BC,
∴∠DPQ=∠PQM,
∴△DQP∽△PMQ,
∴$\frac{PD}{PQ}$=$\frac{PQ}{MQ}$,
∴PQ2=PD×MQ,
∴PM2+MQ2=MD×MQ,
∵CM=$\frac{16-4t}{5}$,
∴MQ=CM-CQ=$\frac{16-9t}{5}$.
∴($\frac{12-3t}{5}$)2+($\frac{16-9t}{5}$)2=5×$\frac{16-9t}{5}$,
∴t=0(舍)或t=$\frac{3}{2}$.
点评 此题是几何变换综合题,主要考查三角形相似,勾股定理,用方程的思想是解本题的关键,难点是用t表示相关线段.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
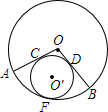 如图,在⊙O中,圆心角∠AOB=120°,⊙O′与OA、OB相切于点C、D,与$\widehat{AB}$相切于F,求$\widehat{AB}$的长与⊙O′的周长的比.
如图,在⊙O中,圆心角∠AOB=120°,⊙O′与OA、OB相切于点C、D,与$\widehat{AB}$相切于F,求$\widehat{AB}$的长与⊙O′的周长的比.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com