
分析 (1)原式利用加减法则计算即可得到结果;
(2)原式利用减法法则变形,计算即可得到结果;
(3)原式结合后,相加即可得到结果;
(4)原式结合后,相加即可得到结果;
(5)原式结合后,相加即可得到结果;
(6)原式利用减法法则变形,计算即可得到结果.
解答 解:(1)原式=-7+8=1;
(2)原式=23-17+7-16=-3;
(3)原式=1-1-$\frac{1}{5}$=-$\frac{1}{5}$;
(4)原式=(-26.54-18.54)+(-6.4+6.4)=45.08;
(5)原式=-12-8+$\frac{6}{5}$-$\frac{7}{10}$=-20+$\frac{1}{2}$=-19$\frac{1}{2}$;
(6)原式=49+20.6-0.6=49+20=69.
点评 此题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
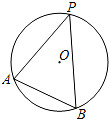 如图,⊙O是△ABP的外接圆,半径r=2,∠APB=45°,则弦AB的长为( )
如图,⊙O是△ABP的外接圆,半径r=2,∠APB=45°,则弦AB的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,把一根绳子对折成线段AB,从P处把绳子剪断,已知AP=$\frac{1}{3}$PB,若剪断后的各段绳子中最长的一段为60cm,则绳子的原长为200cm.
如图所示,把一根绳子对折成线段AB,从P处把绳子剪断,已知AP=$\frac{1}{3}$PB,若剪断后的各段绳子中最长的一段为60cm,则绳子的原长为200cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $x>\frac{5}{2}$ | B. | $x<\frac{5}{2}$ | C. | $x≥\frac{2}{5}$ | D. | $x≥\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com