
【题目】如图,已知直线AB∥CD∥EF,∠POQ=90°,它的顶点O在CD上,两边分别与AB、EF相交于点P、点Q,射线OC始终在∠POQ的内部.
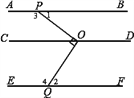
(1)求∠1+∠2的度数;
(2)直接写出∠3与∠4的数量关系;
(3)若∠POQ的度数为α,且0°<α<180°,其余条件不变,猜想∠3与∠4的数量关系(用含α的式子表示);并说明理由.
【答案】(1)∠1+∠2=90°;(2)∠3+∠4=270°;(3)∠3+∠4=360°-α, 理由见解析.
【解析】试题分析:(1)由AB与CD平行,利用两直线平行得到一对内错角相等,由CD与EF平行,同理得到一对内错角相等,而∠POQ=∠POC+∠QOC=90°,等量代换即可求出∠1+∠2的度数;
(2)由∠APB与∠EQF为两个平角,得到∠1+∠3+∠4+∠2=360°,由(1)求出的∠1+∠2的度数即可得到∠3+∠4的度数;
(3)由AB与CD平行,利用两直线平行得到一对内错角相等,由CD与EF平行,同理得到一对内错角相等,而∠POQ=∠POC+∠QOC=90°,等量代换即可求出∠1+∠2=α,由∠APB与∠EQF为两个平角,得到∠1+∠3+∠4+∠2=360°,由∠1+∠2=α即可得到∠3+∠4的度数.
试题解析:(1)∵AB∥CD,
∴∠1=∠POC,
∵CD∥EF,
∴∠2=∠QOC,
∵∠POQ=∠POC+∠QOC=90°,
∴∠1+∠2=90°;
(2)∵∠1+∠3=180°,∠4+∠2=180°,
∴∠1+∠3+∠4+∠2=360°,
又∵∠1+∠2=90°,
∴∠3+∠4=270°;
(3))∵AB∥CD,
∴∠1=∠POC,
∵CD∥EF,
∴∠2=∠QOC,
∵∠POQ=∠POC+∠QOC=α,
∴∠1+∠2=α;
∵∠1+∠3=180°,∠4+∠2=180°,
∴∠1+∠3+∠4+∠2=360°,
又∵∠1+∠2=α,
∴∠3+∠4=360°-α.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
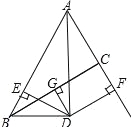
【题目】已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
①求证:BE=CF;
②若AF=5,BC=6,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
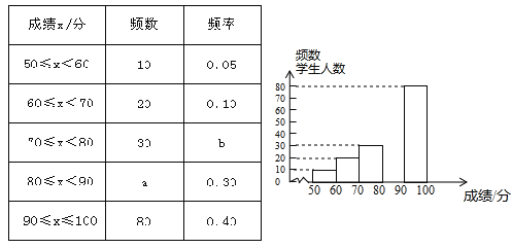
请根据所给信息,解答下列问题:
(1)a=________ , b=________ ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在________ 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有 人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,纸上有5个边长为1的小正方形组成的纸片,可以把它剪拼成一个正方形.
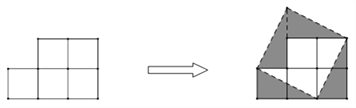
(1)拼成的正方形的面积与边长分别是多少?
(2)请你在3×3的正方形方格图中,连接四个点组成面积为5的正方形.
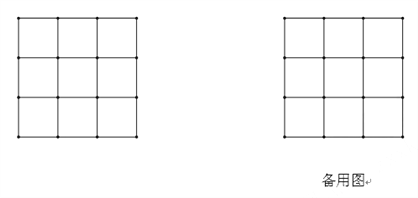
(3)请你把这十个小正方形组成的图形纸,剪开并拼成一个面积为10的正方形.
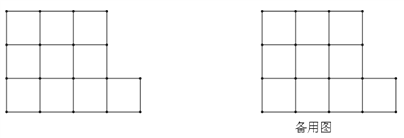
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三角形的两边长分别是3cm和4cm,则第三边长x的取值范围是__________.若x是奇数,则x的值是______;则它的周长为______;若x是偶数,则x的值是______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com