
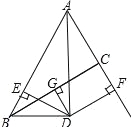
【题目】已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
①求证:BE=CF;
②若AF=5,BC=6,求△ABC的周长.
【答案】①证明详见解析;②16.
【解析】
试题分析:①连接CD,根据垂直平分线性质可得BD=CD,可证Rt△BDE≌Rt△CDF,可得BE=CF;
②根据Rt△ADE≌Rt△ADF得出AE=AF解答即可.
试题解析:①证明:连结CD,
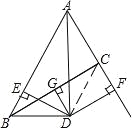
∵D在BC的中垂线上,
∴BD=CD,
∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠DCF=90°,
在RT△BDE和RT△CDF中,DE=DF,BD=CD,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF;
②解:由(HL)可得,Rt△ADE≌Rt△ADF,
∴AE=AF=5,
∴△ABC的周长=AB+BC+AC=(AE+BE)+BC+(AF﹣CF)=5+6+5=16.


科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 对角线互相平分的四边形是平行四边形
B. 对角线相等的四边形是矩形
C. 对角线互相垂直的四边形是菱形
D. 对角线互相垂直的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )(1)带根号的数都是无理数;(2)立方根等于本身的数是0和1;(3)﹣a一定没有平方根;(4)实数与数轴上的点是一一对应的;(5)两个无理数的差还是无理数.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
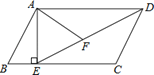
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的周长是20 cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为68 cm2,那么矩形ABCD的面积是_______cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形按边的关系可分为_________和___________,而等腰三角形又分
为___________________和_____________.三角形按内角大小可为___________、____________和_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD∥EF,∠POQ=90°,它的顶点O在CD上,两边分别与AB、EF相交于点P、点Q,射线OC始终在∠POQ的内部.
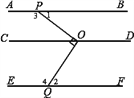
(1)求∠1+∠2的度数;
(2)直接写出∠3与∠4的数量关系;
(3)若∠POQ的度数为α,且0°<α<180°,其余条件不变,猜想∠3与∠4的数量关系(用含α的式子表示);并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空完成推理过程:如图,已知AB⊥BC于点B, BC⊥CD于点C,∠1=∠2.试判断BE与CF的关系,并说明你的理由。
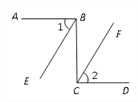
解: _________________.
理由:∵AB⊥BC,BC⊥CD( ),
∴ ∠ABC =_________=90°( )
∵∠1=∠2( ),
∴∠ABC -∠1=∠BCD -∠2 即:∠EBC=∠BCF
∴_________//_________ ( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com