
【题目】如图,在平面直角坐标系xOy中,A为x轴上一点,以OA为直径的作半圆M,点B为OA上一点,以OB为边作□OBDC交半圆M于C,D两点.
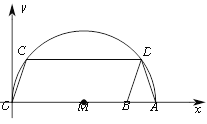
(1)连接AD,求证:DA=DB;
(2)若A点坐标为(20,0),点B的坐标是(16,0),求点C的坐标.
【答案】(1)详见解析;(2)点B的坐标是(2,6)
【解析】
(1)运用平行四边形的性质、四边形的内接圆以及等腰三角形的性质作答即可;
(2) 作DE⊥x轴于点E,延长DC交y轴于点F,连接MD,构造直角三角形,运用勾股定理解答即可.
(1)证明:∵四边形OBDC是平行四边形
∴∠C=∠OBD
∵四边形OADC内接于⊙M
∴∠C+∠A=180°
∵∠OBD+∠ABD=180°
∴∠A=∠ABD
∴DA=DB

(2)作DE⊥x轴于点E,延长DC交y轴于点F,连接MD,则AE=BE=2,
∴MD=MA=10,ME=8
在Rt△MDE中,由勾股定理可得DE=6
∵BD=OC,CF=DE=6
∴△OCF≌△DBE (HL)
∴CF=BE=2
故点B的坐标是(2,6)


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】
(已有经验)
我们已经研究过作一个圆经过两个已知点,也研究过作一个圆与已知角的两条边都相切,尺规作图如图所示:
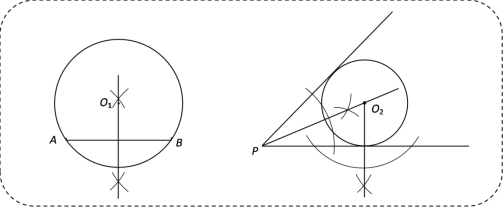
(迁移经验)
(1)如图①,已知点M和直线l,用两种不同的方法完成尺规作图:求作⊙O,使⊙O过M点,且与直线l相切.(每种方法作出一个圆即可,保留作图痕迹,不写作法)

(问题解决)
如图②,在Rt△ABC中,∠C=90°,AC=8,BC=6.
(2)已知⊙O经过点C,且与直线AB相切.若圆心O在△ABC的内部,则⊙O半径r的取值范围为 .
(3)点D是边AB上一点,BD=m,请直接写出边AC上使得∠BED为直角时点E的个数及相应的m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB、BC是半径为![]() 的⊙O内的两条弦,且AB=6,BC=8.(1)若∠ABC=90°,则
的⊙O内的两条弦,且AB=6,BC=8.(1)若∠ABC=90°,则![]() =________;(2)若∠ABC=120°,则
=________;(2)若∠ABC=120°,则![]() =______.
=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形网格中,△ABC和△A'B'C'的顶点都在边长为1的小正方形的格点上.

(1)填空:∠BAC= °,AB= ;
(2)判断:△ABC和△A'B'C这两个三角形相似吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,D是弧![]() 的中点,过点D作DE⊥AC交AC的延长线于点E.
的中点,过点D作DE⊥AC交AC的延长线于点E.
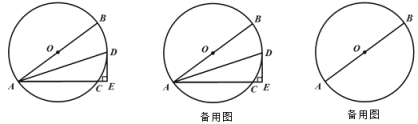
(1)求证:DE是⊙O的切线;
(2)当AB=10,AC=![]() 时,求弧
时,求弧![]() 的长;
的长;
(3)当AB=20时,直接写出△ABC面积最大时,点D到直径AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如表格:
的图象可以得到如表格:
|
|
|
| + | ﹣ |
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如表表格:
的图象可以得到如表表格:
|
|
|
|
| + | ﹣ | + |
由表格可知不等式![]() 的解集为 .
的解集为 .
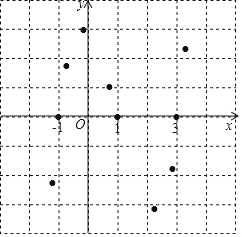
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() (x+1)的图象;
(x+1)的图象;
观察函数![]() 的图象补全下面的表格:
的图象补全下面的表格:
|
|
|
|
|
| + | ﹣ |
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
……
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
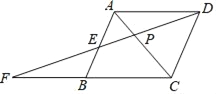
【题目】如图,在菱形ABCD中,P是对角线AC上的一点,连结DP并延长交AB于点E,交CB的延长线于点F.若DP=3,EF=![]() ,则PE的长是( )
,则PE的长是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com