
����Ŀ��С�����ú����벻��ʽ�Ĺ�ϵ��������![]() (
(![]() Ϊ������)�IJ���ʽ�Ľⷨ������̽����
Ϊ������)�IJ���ʽ�Ľⷨ������̽����
(1)������С����̽�����̣��벹��������
�ٶ��ڲ���ʽ![]() ���۲캯��
���۲캯��![]() ��ͼ����Եõ������
��ͼ����Եõ������
|
|
|
| + | �� |
�ɱ����֪����ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��
�ڶ��ڲ���ʽ![]() ���۲캯��
���۲캯��![]() ��ͼ����Եõ��������
��ͼ����Եõ��������
|
|
|
|
| + | �� | + |
�ɱ����֪����ʽ![]() �Ľ⼯Ϊ ��
�Ľ⼯Ϊ ��
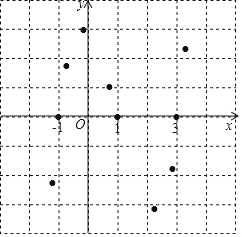
�۶��ڲ���ʽ![]() �������������ĵ㻭������
�������������ĵ㻭������![]() (x+1)��ͼ��
(x+1)��ͼ��
�۲캯��![]() ��ͼ��ȫ����ı���
��ͼ��ȫ����ı���
|
|
|
|
|
| + | �� | �� �� | �� �� |
�ɱ����֪����ʽ![]() �Ľ⼯Ϊ ��
�Ľ⼯Ϊ ��
����
С��������̽�������ܽ����£����ڽ�����![]() (
(![]() Ϊ������)�IJ���ʽ���Ƚ�
Ϊ������)�IJ���ʽ���Ƚ�![]() ���Ӵ�С��˳�����У��ٻ���
���Ӵ�С��˳�����У��ٻ���![]() �ķ�Χ��Ȼ��ͨ���б���İ취�����Է��ֱ�����
�ķ�Χ��Ȼ��ͨ���б���İ취�����Է��ֱ�����![]() �ķ��ų���һ���Ĺ��ɣ�����������ɿ����������IJ���ʽ�Ľ⼯��
�ķ��ų���һ���Ĺ��ɣ�����������ɿ����������IJ���ʽ�Ľ⼯��
(2)����ο�С���ķ�������������⣺
�ٲ���ʽ![]() �Ľ⼯Ϊ ��
�Ľ⼯Ϊ ��
�ڲ���ʽ![]() �Ľ⼯Ϊ ��
�Ľ⼯Ϊ ��
���𰸡�(1)��![]() ��
��![]() ����+; -;
����+; -; ![]() ��
��![]() ��(2)��
��(2)��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() .
.
��������
���������֪�ڱ�����д����Ӧ�ĺ���ֵ�������ԣ�������ж���Ӧ�IJ���ʽ�Ľ⼯.��1���ڸ��ݱ����е����ݿ���ֱ��д������ʽ�Ľ⼯��
�۸��ݱ����е����ݿ���ֱ��д������ʽ�Ľ⼯��
��2���ٸ���С���ķ���������ֱ��д���ò���ʽ�Ľ⼯��
�ڸ���С���ķ���������ֱ��д���ò���ʽ�Ľ⼯��
(1)���ɱ����֪����ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
�۵�![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
�ɱ����֪����ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��![]() ��
��
�ʴ�Ϊ��+������![]() ��
��![]() ��
��
(2)�ٲ���ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��![]() ��
��
�ڲ���ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ����֪ʶ�У����̡�����������ʽ�����Ž��ܵ���ϵ�����Ķ�����������ϣ��ش����⣺
���ú���ͼ���ҷ���![]() ��ķ�Χ.�躯��
��ķ�Χ.�躯��![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() .����
.����![]() ��ͼ��������
��ͼ��������![]() ��
��![]() ������
������![]() ��
��![]() ���·�����
���·�����![]() ��
��![]() ���Ϸ�����ú���ͼ����
���Ϸ�����ú���ͼ����![]() �ύ�������ش���-2��С��-1.�ʣ�����
�ύ�������ش���-2��С��-1.�ʣ�����![]() ���н⣬�Ҹý�ķ�ΧΪ
���н⣬�Ҹý�ķ�ΧΪ![]() .
.
���϶���
��һԪ���β���ʽ![]() .�������������ˣ����Ϊ���ɵã�
.�������������ˣ����Ϊ���ɵã�
�����![]() ����
����![]() ����
����![]()
�����![]() ����
����![]() ������
������
�ʣ�![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() .
.
��1������ݲ���һ������⣺��֪����![]() ��Ψһ��
��Ψһ��![]() ����
����![]() ��
��![]() ��������������
Ϊ��������������![]() ��ֵ.
��ֵ.
��2�����ϲ���һ����϶�������⣺������![]() �ķ���
�ķ���![]() �Ľ�ֱ�Ϊ
�Ľ�ֱ�Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�AΪx����һ�㣬��OAΪֱ��������ԲM����BΪOA��һ�㣬��OBΪ������OBDC����ԲM��C��D���㣮
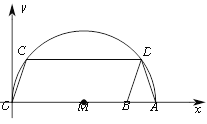
��1������AD����֤��DA��DB��
��2����A������Ϊ��20��0������B�������ǣ�16��0�������C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ABC�У�����C��CD//AB��E��AC���е㣬����DE���ӳ�����AB�ڵ�F����CB���ӳ����ڵ�G������AD��CF��
ABC�У�����C��CD//AB��E��AC���е㣬����DE���ӳ�����AB�ڵ�F����CB���ӳ����ڵ�G������AD��CF��
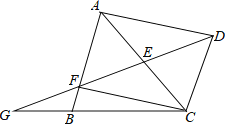
(1)��֤���ı���AFCD��ƽ���ı��Σ�
(2)��GB��3��BC��6��BF��1����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0����y�ύ�ڵ�C����x�ύ��A��B���㣬���е�B������ΪB��4��0���������ߵĶԳ��ύx���ڵ�D��CE��AB�����������ߵĶԳ��ύ�ڵ�E���������н��ۣ���a��0����b��0����4a+2b+c��0����AD+CE��4������������ȷ���۵�����ǡ�_____________________ ����
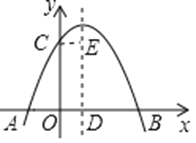
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������8����һ�������Ŀڴ���װ��2����������Ϊ����1������2����1������1��������Щ�����ɫ�ⶼ��ͬ������ҡ�ȣ�
��1��������������1����ǡ����������ĸ����� ��
��2���ȴ�����������1�����ٴ����µ�3��������������1���������оٷ�������״ͼ���б��������ζ���������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������CD��AB�ڵ�E��AM�ǡ�ACD����ǡ�DAF��ƽ���ߣ�

��1����֤��AM����O�����ߣ�
��2������D = 60����AD = 2������CO��AM����N�㣬��д����ON����˼·��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y��x2��ͼ����ͼ��ʾ����֪A������Ϊ��1��1��������A��AA1��x�ύ�������ڵ�A1������A1��A1A2��OA���������ڵ�A2������A2��A2A3��x�ύ�������ڵ�A3������A3��A3A4��OA���������ڵ�A4���������ν�����ȥ�����A2019������Ϊ_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺�����������a��b����a��0��b��0��������IJ���ʽ��![]() �����ҽ���a��bʱȡ���Ⱥ����ǰ�
�����ҽ���a��bʱȡ���Ⱥ����ǰ�![]() ��������a��b������ƽ��������
��������a��b������ƽ��������![]() ��������a��b�ļ���ƽ������������������ʽ�ɱ���Ϊ����������������ƽ������С�ڣ������ڻ���ڣ����ǵļ���ƽ������������ѧ���й㷺��Ӧ�ã��ǽ����ֵ������������ߣ�
��������a��b�ļ���ƽ������������������ʽ�ɱ���Ϊ����������������ƽ������С�ڣ������ڻ���ڣ����ǵļ���ƽ������������ѧ���й㷺��Ӧ�ã��ǽ����ֵ������������ߣ�
����̽������1����֪x��0������y��x+![]() ����Сֵ��
����Сֵ��
����Ǩ�ƣ���2��ѧУ����Χǽһ��Ϊб�ߣ���դ��Χ��һ�����Ϊ100m2��ֱ�������Σ���ΪӢ��ǣ�ֱ�������ε���ֱ�DZ߸�Ϊ����ʱ������դ����̣�
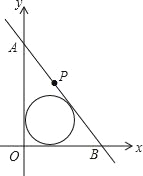
����Ӧ�ã���3����ͼ����ֱ������ϵ�У�ֱ��AB����P��3��4�������������������ཻ��A��B���㣬����AOB�������Сʱ�����AOB������Բ�İ뾶��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com