
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2),C(3,﹣3).
(1)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1.
(2)请画出与△ABC关于y轴对称的△A2B2C2.
(3)请写出A1、A2的坐标.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2,B3…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记a1,第2个等边三角形的边长记为a2,以此类推,若OA1=3,则a2=_______,a2019=_______.
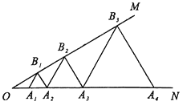
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,F是⊙O外一点,过点F作FD⊥AB于点D,交弦AC于点E,且FC=FE.
(1)求证:FC是⊙O的切线;
(2)若⊙O的半径为5,cos∠FCE=![]() ,求弦AC的长.
,求弦AC的长.
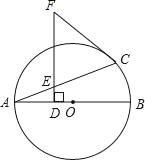
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() ,下列结论错误的是( )
,下列结论错误的是( )
A.若两点A(![]() ),B(
),B(![]() )在该函数图象上,且
)在该函数图象上,且![]() ,则
,则![]()
B.函数的图象不经过第三象限
C.函数的图象向下平移4个单位长度得到![]() 的图象
的图象
D.函数的图象与![]() 轴的交点坐标是(0,4)
轴的交点坐标是(0,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲告诉小明:“距离地面越远,温度越低,”并给小明出示了下面的表格.
距离地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
温度(℃) | 20 | 14 | 8 | 2 | ﹣4 | ﹣10 |
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t是怎么变化的?
(3)你知道距离地面5千米的高空温度是多少吗?
(4)你能猜出距离地面6千米的高空温度是多少吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示),如果大正方形的面积是64,小正方形的面积为4,直角三角形的两直角边长分别为a,b,且a> b . 那么下列结论:(1)a2+b2=64,(2)a-b=2,(3)ab=30,(4)a+b=2![]() .正确结论的个数有( )
.正确结论的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是三个垃圾存放点,点B、C分别位于点A的正北和正东方向,AC=200米,编号为1﹣6号的6名同学分别测得∠C的度数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | |
∠C(单位:度) | 37 | 36 | 37 | 40 | 34 | 38 |
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图,如图:
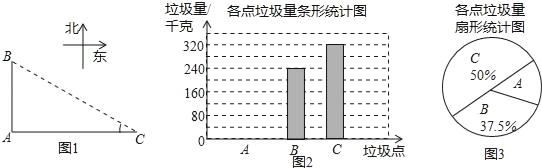
(1)求表中∠C度数的平均数,众数和中位数;
(2)求A处的垃圾量,并将图2补充完整;
(3)用(1)中的![]() 作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用:(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com