
����Ŀ����ƽ��ֱ������ϵxOy�У����κ���y=mx2����m+n��x+n��m��0����ͼ����y�������ύ��A�㣮
��1����֤���ö��κ�����ͼ����x������������㣻
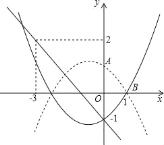
��2����ö��κ�����ͼ����x��������������Ҳ�Ľ���Ϊ��B������ABO=45������ֱ��AB����ƽ��2����λ�õ�ֱ��l����ֱ��l�Ľ���ʽ��
��3���ڣ�2���������£���M��p��q��Ϊ���κ���ͼ���ϵ�һ�����㣬����3��p��0ʱ����M����x��ĶԳƵ㶼��ֱ��l���·�����m��ȡֵ��Χ��
���𰸡���1���ö��κ�����ͼ����������������㣻��2��y=��x��1����3��m��ȡֵ��ΧΪ����![]() ��m��0��
��m��0��
��������
�����������1��ֱ�����ø����б�ʽ�������ȫƽ����ʽ������ķ��Ž����ó��𰸣�
��2���������B��A�����꣬�������ֱ��AB�Ľ���ʽ��������ƽ�ƹ��ɵó��𰸣�
��3�����ݵ���3��p��0ʱ����M����x��ĶԳƵ㶼��ֱ��l���·�����p=0ʱ��q=1����p=��3ʱ��q=12m+4�����ͼ���֪������12m+4����2�����ɵó�m��ȡֵ��Χ��
�����������1����mx2����m+n��x+n=0������=��m+n��2��4mn=��m��n��2��
�����κ���ͼ����y�������ύ��A�㣬��A��0��n������n��0��
����m��0����m��n��0�����=��m��n��2��0��
���ö��κ�����ͼ����������������㣻
��2����mx2����m+n��x+n=0����ã�x1=1��x2=![]() ���ɣ�1����
���ɣ�1����![]() ��0����B������Ϊ��1��0����
��0����B��������1��0����
������ABO=45����
����A��0��1������n=1��
������ֱ��AB�Ľ���ʽΪ��y=��x+1��
������ƽ��2����λ�ɵõ�ֱ��l��y=��x��1��
��3���ɣ�2���ö��κ����Ľ���ʽΪ��y=mx2����m+1��x+1��
��M��p��q�� Ϊ���κ���ͼ���ϵ�һ�����㣬
��q=mp2����m+1��p+1��
����M������ĶԳƵ�M��������Ϊ��p����q����
��M�����ڶ��κ���y=��m2+��m+1��x��1�ϣ�
������3��p��0ʱ����M����x��ĶԳƵ㶼��ֱ��l���·���
��p=0ʱ��q=1����p=��3ʱ��q=12m+4��
���ͼ���֪������12m+4����2����ã�m����![]() ��
��
��m��ȡֵ��ΧΪ����![]() ��m��0��
��m��0��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ÿ�ѧ��������ʾ���и�����
0.0001��0.00013��0.000000204����0.00000000406��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
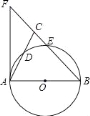
����Ŀ����ͼ���ڡ�ABC�У�BA=BC����ABΪֱ���ġ�O�ֱ�AC��BC�ڵ�D��E��BC���ӳ����ڡ�O������AF���ڵ�F��
��1����֤����ABC=2��CAF��
��2����AC=2![]() ��CE��EB=1��4����CE�ij���
��CE��EB=1��4����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B�������xǧ�ף��״�A���Ҵ�B��ͬʱ������������У��ס�����ʻ���ٶȷֱ�Ϊuǧ��/Сʱ��vǧ��/Сʱ�����У��ٳ�����30�����������ڼ�B����������أ�����ʱ�־�����30���ӣ��۵�������ʱ������A����4ǧ�ף���x��u��v���������⣬�������ۣ�����λͬѧ���õ���3���������£����д����һ���ǣ�������
A.x=u+4
B.x=v+4
C.2x-u=4
D.x-v=4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ƻ�����4��ѡ�Σ����֡��滭���������赸��ѧУ��ȡ��������ķ��������ʾ����飨ÿ���������ѧ������ѡ�����ֻ��ѡ������һ�ţ����Ե���������ͳ�ƺ��������²�����������ͳ��ͼ��
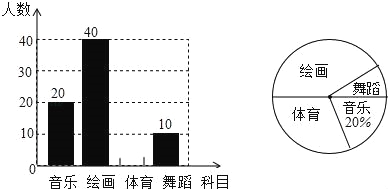
��������ͳ��ͼ�ṩ����Ϣ���ش��������⣺
��1���˴ε����ȡ��ѧ������Ϊa= �ˣ�����ѡ�����滭����ѧ������ռ���������İٷֱ�Ϊb= 4 ��
��2����ȫ����ͳ��ͼ��
��3������У��2000��ѧ���������ȫУѡ�����滭����ѧ����Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3�֣�һֻ�����Ĵ�����װ��4������2������ÿ�������ɫ�ⶼ��ͬ��������������3���������¼�Ϊ��Ȼ�¼����ǣ� ��
A��������1�����Ǻ���
B��������1�����ǰ���
C��������2�����Ǻ���
D��������2�����ǰ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������̫�����ͶӰ�µõ��ļ���ͼ��һ���ǣ� ��
A. ������ B. ƽ���ı��λ��߶� C. ���� D. ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������εij���5cm �� ����2b cm �� �ܳ�Ϊa cm �� �г���������ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������12�꣬��үү60�꣬���������������Ժ�үү��������С����4����
A. 2 B. 4 C. 6 D. 8
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com