
ЁОЬтФПЁПвбжЊЃКдкФкНЧВЛШЗЖЈЕФЁїABCжаЃЌABЃНACЃЌЕуEЁЂFЗжБ№дкABЁЂACЩЯЃЌEFЁЮBCЃЌЦНаавЦЖЏEFЃЌШчЙћЬнаЮEBCFгаФкЧадВЃЎ
ЕБ![]() ЃН
ЃН![]() ЪБЃЌsinBЃН
ЪБЃЌsinBЃН![]() ЃЛ
ЃЛ
ЕБ![]() ЃН
ЃН![]() ЪБЃЌsinBЃН
ЪБЃЌsinBЃН![]() (ЬсЪОЃК
(ЬсЪОЃК![]() ЃН
ЃН![]() )ЃЛЕБ
)ЃЛЕБ![]() ЃН
ЃН![]() ЪБЃЌsinBЃН
ЪБЃЌsinBЃН![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧыФуИљОнвдЩЯЫљЗДгГЕФЙцТЩЃЌЬюПеЃКЕБ![]() ЃН
ЃН![]() ЪБЃЌsinBЕФжЕЕШгк______ЃЛ
ЪБЃЌsinBЕФжЕЕШгк______ЃЛ
ЃЈ2ЃЉЕБ![]() ЃН
ЃН![]() ЪБ(nЪЧДѓгк1ЕФздШЛЪ§)ЃЌЧыгУКЌnЕФДњЪ§ЪНБэЪОsinBЃН______ЃЌВЂЛГіЭМаЮЁЂаДГівбжЊЁЂЧѓжЄКЭжЄУїЙ§ГЬЃЎ
ЪБ(nЪЧДѓгк1ЕФздШЛЪ§)ЃЌЧыгУКЌnЕФДњЪ§ЪНБэЪОsinBЃН______ЃЌВЂЛГіЭМаЮЁЂаДГівбжЊЁЂЧѓжЄКЭжЄУїЙ§ГЬЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЌжЄУїМћНтЮіЃЎ
ЃЌжЄУїМћНтЮіЃЎ
ЁОНтЮіЁП
(1) ![]() ЕФЗжФИМг1МДЪЧsinBЕФЗжФИЃЌsinBЕФЗжзгЪЧ2ГЫвд
ЕФЗжФИМг1МДЪЧsinBЕФЗжФИЃЌsinBЕФЗжзгЪЧ2ГЫвд![]() ЕФЗжФИЕФЫуЪѕЦНЗНИљЃЌИљОнЙцТЩжБНгаДГіД№АИМДПЩЃЛ
ЕФЗжФИЕФЫуЪѕЦНЗНИљЃЌИљОнЙцТЩжБНгаДГіД№АИМДПЩЃЛ
(2) гЩвбжЊЬѕМўЯШаДГівбжЊКЭЧѓжЄЃЌдйНјаажЄУїЃК
вЊЯыБэЪОГіsinBЃЌашжЄУїЁїAEMЁзЁїABNЃЌЕУГі![]() ЃЌдйЩшEM=kЃЌдђBN=nkЃЌзїEHЁЮMNНЛBCгкHЃЌдђHN=EM=kЃЎгЩЙДЙЩЖЈРэЕУ
ЃЌдйЩшEM=kЃЌдђBN=nkЃЌзїEHЁЮMNНЛBCгкHЃЌдђHN=EM=kЃЎгЩЙДЙЩЖЈРэЕУ![]() ЃЌМДПЩЕУГіsinBЕФжЕЃЛ
ЃЌМДПЩЕУГіsinBЕФжЕЃЛ
НтЃК(1)ИљОнЙцТЩЃЌЕБ![]() ЃН
ЃН![]() ЪБЃЌ
ЪБЃЌ
sinB=![]() ЃЌ
ЃЌ
ЙЪЕБ![]() ЃН
ЃН![]() ЪБЃЌsinBЕФжЕЕШгк
ЪБЃЌsinBЕФжЕЕШгк![]() ЁЁ
ЁЁ
(2)![]() ЃЎ
ЃЎ
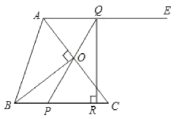
вбжЊЃКдкЁїABCжаЃЌABЃНACЃЌEFЁЮBCЃЌЁбOФкЧагкЬнаЮEBCFЃЌЕуDЁЂNЁЂGЁЂMЮЊЧаЕуЃЌ![]() ЃН
ЃН![]() ЪБ(nЪЧДѓгк1ЕФздШЛЪ§)ЃЌШчЯТЭМЃЎ
ЪБ(nЪЧДѓгк1ЕФздШЛЪ§)ЃЌШчЯТЭМЃЎ
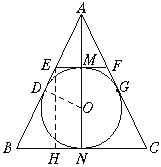
ЧѓжЄЃКsinBЃН![]() ЃЎ
ЃЎ
жЄУїЃКСЌНсAOВЂбгГЄгыBCЯрНЛЃЎ
ЁпЁЁЁбOФкЧагкЬнаЮEBCFЃЌABЁЂACЪЧЁбOЕФЧаЯпЃЌ
ЁрЁЁЁЯBAOЃНЁЯCAOЃЌ
ЁпЁЁEFЁЮBCЃЌABЃНACЃЌ
ЁрЁЁAEЃНAFЃЎ
гжЁпMЁЂNЮЊЧаЕуЃЌ
ЁрЁЁOMЁЭEFЃЌONЁЭBCЃЎ
ЁрЁЁAOЁЭEFгкMЃЌAOЁЭBCгкNЃЎ
ЁпЁЁEFЁЮBCЃЌ
ЁрЁЁEMЁЮBNЃЎ
ЁрЁЁЁїAEMЁзЁїABNЃЌ
ЁрЁЁ![]() ЃЌ
ЃЌ
ЩшEMЃНkЃЌдђBNЃНnkЃЎ
зїEHЁЮMNНЛBCгкHЃЌдђHNЃНEMЃНkЃЎ
ЁпЁЁDЁЂNЁЂMЮЊЧаЕуЃЌ
ЁрЁЁBDЃНBNЃНnkЃЌEDЃНEMЃНkЃЎ
дкЁїEHBжаЃЌЁЯEHBЃНЁЯMNBЃН90ЁуЃЌ
BEЃНBDЃЋDEЃН(nЃЋ1)kЃЌ
BHЃНBN-HNЃН(n-1)kЃЎ
гЩЙДЙЩЖЈРэЃЌЕУEHЃН2![]() ЁЄkЃЎ
ЁЄkЃЎ
ЁрsinBЃН![]() ЃЎ
ЃЎ


 аЁбЇПЮЬУзївЕЯЕСаД№АИ
аЁбЇПЮЬУзївЕЯЕСаД№АИ Н№ВЉЪПвЛЕуШЋЭЈЯЕСаД№АИ
Н№ВЉЪПвЛЕуШЋЭЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮїАВЪаФГбЇаЃдкЁАЮвУЧШчКЮдЄЗРИаШОаТаЭЙкзДВЁЖОЁБаћНВХрбЕКѓЃЌЖдбЇЩњжЊЯўЧщПіНјааСЫвЛДЮВтЪдЃЌЦфВтЪдГЩМЈАДееБъзМЛЎЗжЮЊЫФИіЕШМЖЃК![]() гХауЃЌ
гХауЃЌ![]() СМКУЃЌ
СМКУЃЌ![]() КЯИёЃЌ
КЯИёЃЌ![]() ВЛКЯИёЃЎЮЊСЫСЫНтИУаЃбЇЩњЕФГЩМЈзДПіЃЌЖддкаЃбЇЩњНјааЫцЛњГщбљЕїВщЃЌВЂЖдЕїВщНсЙћНјааЭГМЦЃЌШчЭМЫљЪОЃЎ
ВЛКЯИёЃЎЮЊСЫСЫНтИУаЃбЇЩњЕФГЩМЈзДПіЃЌЖддкаЃбЇЩњНјааЫцЛњГщбљЕїВщЃЌВЂЖдЕїВщНсЙћНјааЭГМЦЃЌШчЭМЫљЪОЃЎ
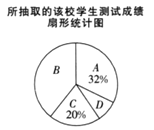

ЧыНсКЯЭГМЦЭМЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉИУаЃГщбљЕїВщЕФбЇЩњШЫЪ§ЮЊ___________ЃЎ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ3ЃЉбљБОжаЃЌбЇЩњГЩМЈЕФжаЮЛЪ§ЫљдкЕШМЖЪЧ______ЃЎ(ЬюЁА![]() ЁБЁЂЁА
ЁБЁЂЁА![]() ЁБЁЂЁА
ЁБЁЂЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБ)
ЁБ)
ЃЈ4ЃЉИУаЃЙВгабЇЩњ2500ШЫЃЌЙРМЦШЋаЃВтЪдГЩМЈЮЊгХауКЭСМКУЕФбЇЩњЙВга______ШЫЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
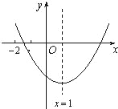
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓШчЭМЫљЪОЃЌгаЯТСаНсТлЃК
Ђйb2Љ4acЃО0ЃЛЂкabcЃО0ЃЛЂл8a+cЃО0ЃЛЂм9a+3b+cЃМ0ЃЎ ЦфжаЃЌе§ШЗНсТлЕФга_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЊдкНЫеЪЁФГСжГЁЖЋЮїЗНЯђЕФСНЕижЎМфаовЛЬѕЙЋТЗMNЃЌвбжЊCЕужмЮЇ200УзЗЖЮЇФкЮЊдЪМЩСжБЃЛЄЧјЃЌдкMNЩЯЕФЕуAДІВтЕУCдкAЕФББЦЋЖЋ45ЁуЗНЯђЩЯЃЌДгAЯђЖЋзп600УзЕНДяBДІЃЌВтЕУCдкЕуBЕФББЦЋЮї60ЁуЗНЯђЩЯЃЎ

ЃЈ1ЃЉMNЪЧЗёДЉЙ§дЪМЩСжБЃЛЄЧјЃПЮЊЪВУДЃПЃЈВЮПМЪ§ОнЃК![]() ЃЉ
ЃЉ
ЃЈ2ЃЉШєаоТЗЙЄГЬЙЄГЬашОЁПьЭъГЩЃЎШчЙћгЩМзЁЂввСНИіЙЄГЬЖгКЯзіЃЌ12ЬьПЩЭъГЩЃЛШчЙћгЩМзЁЂввСНЖгЕЅЖРзіЃЌМзЖгБШввЖгЩйгУ10ЬьЭъГЩЃЎЧѓМзЁЂввСНЙЄГЬЖгЕЅЖРЭъГЩДЫЯюЙЄГЬЫљашЕФЬьЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮЭјИёЩЯга6ИіаБШ§НЧаЮЃКЂйЁїABCЃЛЂкЁїCDBЃЛЂлЁїDEBЃЛЂмЁїFBGЃЛЂнHGFЃЛЂоЁїEKFЃЎЧыФуаДГігыЁїABCЯрЫЦЕФШ§НЧаЮЃЌВЂаДГіМђвЊЕФжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаФГжабЇЛ§МЋЯьгІДДНЈШЋЙњЮФУїГЧЪаЛюЖЏЃЌОйАьСЫвдЁАаЃдАЮФУїЁБЮЊжїЬтЕФЪжГБЈБШШќ.ЫљгаВЮШќзїЦЗОљЛёНБЃЌНБЯюЗжЮЊвЛЕШНБЁЂЖўЕШНБЁЂШ§ЕШНБКЭгХауНБЃЌНЋЛёНБНсЙћЛцжЦГЩШчгвСНЗљЭГМЦЭМ.ЧыФуИљОнЭМжаЫљИјаХЯЂНтД№втЃЉ
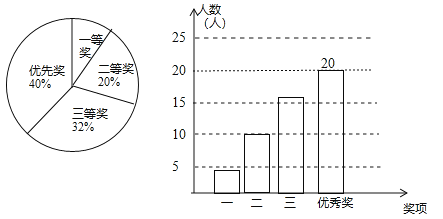
ЃЈ1ЃЉЕШНБЫљеМЕФАйЗжБШЪЧ________ЃЛШ§ЕШНБЕФШЫЪ§ЪЧ________ШЫЃЛ
ЃЈ2ЃЉОнЭГМЦЃЌдкЛёЕУвЛЕШНБЕФбЇЩњжаЃЌФаЩњгыХЎЩњЕФШЫЪ§БШЮЊ![]() ЃЌбЇаЃМЦЛЎбЁХЩ1УћФаЩњКЭ1УћХЎЩњВЮМгЪаЪжГБЈБШШќЃЌЧыЧѓГіЫљбЁ2ЮЛЭЌбЇЧЁЪЧ1УћФаЩњКЭ1УћХЎЩњЕФИХТЪЃЛ
ЃЌбЇаЃМЦЛЎбЁХЩ1УћФаЩњКЭ1УћХЎЩњВЮМгЪаЪжГБЈБШШќЃЌЧыЧѓГіЫљбЁ2ЮЛЭЌбЇЧЁЪЧ1УћФаЩњКЭ1УћХЎЩњЕФИХТЪЃЛ
ЃЈ3ЃЉбЇаЃМЦЛЎДгЛёЕУЖўЕШНБЕФЭЌбЇжабЁШЁвЛВПЗжШЫНјааМЏбЕЪЙЦфЬсЩ§ЮЊвЛЕШНБЃЌвЊЪЙЛёЕУвЛЕШНБЕФШЫЪ§ВЛЩйгкЖўЕШНБШЫЪ§ЕФ2БЖЃЌФЧУДжСЩйбЁШЁЖрЩйШЫНјааМЏбЕЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїЩфЯп
зїЩфЯп![]() ЃЌЕу
ЃЌЕу![]() ЪЧБп
ЪЧБп![]() ЩЯШЮвтвЛЕуЃЌСЌНг
ЩЯШЮвтвЛЕуЃЌСЌНг![]() ВЂбгГЄгыЩфЯп
ВЂбгГЄгыЩфЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() СНЕужЎМфЕФОрРыЮЊ
СНЕужЎМфЕФОрРыЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЕФДЙЯпЃЌДЙзуЮЊ
ЕФДЙЯпЃЌДЙзуЮЊ![]() ЃЎсЏсЏЭЌбЇЫМПМКѓИјГіСЫЯТУцЮхЬѕНсТлЃЌе§ШЗЕФЙВгаЃЈ ЃЉ
ЃЎсЏсЏЭЌбЇЫМПМКѓИјГіСЫЯТУцЮхЬѕНсТлЃЌе§ШЗЕФЙВгаЃЈ ЃЉ
Ђй![]() ЃЛ
ЃЛ
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛ
ЃЛ
ЂлЕБ![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
ЂмЕБ![]() Лђ
Лђ![]() ЪБЃЌЖМга
ЪБЃЌЖМга![]() ЃЛ
ЃЛ
ЂнЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() вЛЖЈЯрЫЦЃЎ
вЛЖЈЯрЫЦЃЎ
A.2ЬѕB.3ЬѕC.4ЬѕD.5Ьѕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкбЇЯАНтжБНЧШ§НЧаЮвдКѓЃЌФГаЫШЄаЁзщВтСПСЫЦьИЫЕФИпЖШЃЎШчЭМЃЌФГвЛЪБПЬЃЌЦьИЫABЕФгАзгвЛВПЗжТфдкЫЎЦНЕиУцLЕФгАГЄBCЮЊ5УзЃЌТфдкаБЦТЩЯЕФВПЗжгАГЄCDЮЊ4УзЃЎВтЕУаБCDЕФЦТЖШiЃН1ЃК![]() ЃЎЬЋбєЙтЯпгыаБЦТЕФМаНЧЁЯADCЃН80ЁуЃЌдђЦьИЫABЕФИпЖШ_____ЃЎЃЈОЋШЗЕН0.1УзЃЉЃЈВЮПМЪ§ОнЃКsin50ЁуЃН0.8ЃЌtan50ЁуЃН1.2ЃЌ
ЃЎЬЋбєЙтЯпгыаБЦТЕФМаНЧЁЯADCЃН80ЁуЃЌдђЦьИЫABЕФИпЖШ_____ЃЎЃЈОЋШЗЕН0.1УзЃЉЃЈВЮПМЪ§ОнЃКsin50ЁуЃН0.8ЃЌtan50ЁуЃН1.2ЃЌ![]() ЃН1.732ЃЉ
ЃН1.732ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЭЦГівЛПюаТВњЦЗЃЌЭЈЙ§ЪаГЁЕїбаКѓЃЌАДШ§жжбеЩЋЪмЛЖгЕФГЬЖШЗжБ№ЖдAбеЩЋЁЂBбеЩЋЁЂCбеЩЋЕФВњЦЗдкГЩБОЕФЛљДЁЩЯЗжБ№МгМл40%ЃЌ50%ЃЌ60%ГіЪлЃЈШ§жжбеЩЋВњЦЗЕФГЩБОвЛбљЃЉЃЌОЙ§вЛИіМОЖШЕФОгЊКѓЃЌЗЂЯжCбеЩЋВњЦЗЕФЯњСПеМзмЯњСПЕФ40%ЃЌШ§жжбеЩЋВњЦЗЕФзмРћШѓТЪЮЊ51.5%ЃЌЕкЖўИіМОЖШЃЌЙЋЫООіЖЈЖдAВњЦЗНјааЩ§МЖЃЌЩ§МЖКѓAВњЦЗЕФГЩБОЬсИпСЫ25%ЃЌЦфЯњСПЬсИпСЫ60%ЃЌРћШѓТЪЮЊдРДЕФСНБЖЃЛBВњЦЗЕФЯњСПЬсИпЕНгыЩ§МЖКѓЕФAВњЦЗЕФЯњСПвЛбљЃЌCВњЦЗЕФЯњСПБШЕквЛМОЖШЬсИпСЫ50%ЃЌдђЕкЖўИіМОЖШЕФзмРћШѓТЪЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com