
【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线![]() :
:![]() 与
与![]() :
:![]() 为“友好抛物线”.
为“友好抛物线”.
(1)求抛物线![]() 的解析式.
的解析式.
(2)点A是抛物线![]() 上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线![]() 的顶点为C,点B的坐标为(﹣1,4),问在
的顶点为C,点B的坐标为(﹣1,4),问在![]() 的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线
的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线![]() 上?若存在求出点M的坐标,不存在说明理由.
上?若存在求出点M的坐标,不存在说明理由.
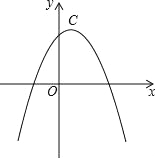
【答案】(1) ![]() ;(2) 当a=
;(2) 当a=![]() 时,AQ+OQ有最大值,最大值为
时,AQ+OQ有最大值,最大值为![]() (3)存在点M,(1,2)或(1,5).
(3)存在点M,(1,2)或(1,5).
【解析】
试题分析:(1)先求得![]() 顶点坐标,然后依据两个抛物线的顶点坐标相同可求得m、n的值;
顶点坐标,然后依据两个抛物线的顶点坐标相同可求得m、n的值;
(2)设A(a,![]() ).则OQ=x,AQ=
).则OQ=x,AQ=![]() ,然后得到OQ+AQ与a的函数关系式,最后依据配方法可求得OQ+AQ的最值;
,然后得到OQ+AQ与a的函数关系式,最后依据配方法可求得OQ+AQ的最值;
(3)连接BC,过点B′作B′D⊥CM,垂足为D.接下来证明△BCM≌△MDB′,由全等三角形的性质得到BC=MD,CM=B′D,设点M的坐标为(1,a).则用含a的式子可表示出点B′的坐标,将点B′的坐标代入抛物线的解析式可求得a的值,从而得到点M的坐标.
试题解析:(1)∵![]() =
=![]() ,
,
∴抛物线![]() 的顶点坐标为(1,4).
的顶点坐标为(1,4).
∵抛物线![]() 与
与![]() 顶点相同,
顶点相同,
∴![]() =1,﹣1+m+n=4.
=1,﹣1+m+n=4.
解得:m=2,n=3.
∴抛物线![]() 的解析式为
的解析式为![]() ;
;
(2)如图1所示:

设点A的坐标为(a,![]() ).
).
∵AQ=![]() ,OQ=a,
,OQ=a,
∴AQ+OQ=![]() +a=
+a=![]() =
=![]() .
.
∴当a=![]() 时,AQ+OQ有最大值,最大值为
时,AQ+OQ有最大值,最大值为![]() .
.
(3)存在点M,理由如下:
如图2所示;连接BC,过点B′作B′D⊥CM,垂足为D.

∵B(﹣1,4),C(1,4),抛物线的对称轴为x=1,
∴BC⊥CM,BC=2.
∵∠BMB′=90°,
∴∠BMC+∠B′MD=90°.
∵B′D⊥MC,
∴∠MB′D+∠B′MD=90°.
∴∠MB′D=∠BMC.
在△BCM和△MDB′中,∠MB′D=∠BMC ,∠BCM=∠MDB′,BM=MB′,
∴△BCM≌△MDB′.
∴BC=MD,CM=B′D.
设点M的坐标为(1,a).则B′D=CM=4﹣a,MD=CB=2.
∴点B′的坐标为(a﹣3,a﹣2).
∴![]() ,
,
整理得:![]() ﹣7a+10=0.
﹣7a+10=0.
解得a=2,或a=5.
当a=2时,M的坐标为(1,2),
当a=5时,M的坐标为(1,5).
综上所述当点M的坐标为(1,2)或(1,5)时,B′恰好落在抛物线![]() 上.
上.


科目:初中数学 来源: 题型:
【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 调查某省中学生的身高情况,适宜采用全面调查
B. 篮球队员在罚球线上投篮两次都未投中,这是不可能事件
C. 天气预报说明天的降水概率为95%,意味着明天一定下雨
D. 任意买一张电影票,座位号是2的倍数,这是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=![]() x2﹣bx+c与x轴交于点A(8,0)、B(2,0)两点,与y轴交于点C.
x2﹣bx+c与x轴交于点A(8,0)、B(2,0)两点,与y轴交于点C.
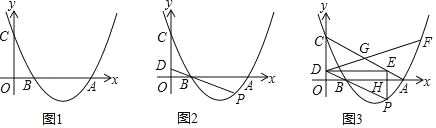
(1)如图1,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点,连接PB并延长交y轴于点D,若点P的横坐标为t,CD长为d,求d与t的函数关系式(并求出自变量t的取值范围);
(3)如图3,在(2)的条件下,连接AC,过点P作PH⊥x轴,垂足为点H,延长PH交AC于点E,连接DE,射线DP关于DE对称的射线DG交AC于点G,延长DG交抛物线于点F,当点G为AC中点时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0, a),C(b,0)满足![]() 。
。
(1)则C点的坐标为__________;A点的坐标为__________.
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.AC的中点D的坐标是(1,2),设运动时间为t(t>0)秒.问:是否存在这样的t,使![]() ,若存在,请求出t的值;若不存在,请说明理由.
,若存在,请求出t的值;若不存在,请说明理由.
(3)点F是线段AC上一点,满足∠FOC=∠FCO, 点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H, 当点E在线段OA上运动的过程中,![]() 的值是否会发生变化,若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化,若不变,请求出它的值;若变化,请说明理由.
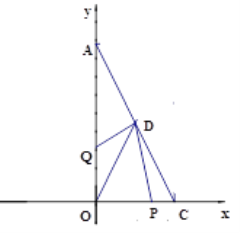
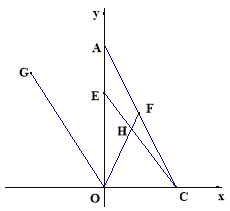
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知规定一种新运算:x※y=xy+1;x★y=x+y﹣1,例如:2※3=2×3+1=7;2★3=2+3﹣1=4.若a※(4★5)的值为17,且a※x=a★6,则x的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com