
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 根据一元二次方程的根与系数的关系求得m的值后,再求得方程的解,求出较小锐角的正弦值.
解答 解:∵a,b是方程x2-mx+2m-2=0的解,
∴a+b=m,ab=2m-2,
在Rt△ABC中,由勾股定理得,a2+b2=c2,
而a2+b2=(a+b)2-2ab,c=5,
∴a2+b2=(a+b)2-2ab=25,
即:m2-2(2m-2)=25
解得,m1=7,m2=-3,
∵a,b是Rt△ABC的两条直角边的长.
∴a+b=m>0,m=-3不合题意,舍去.
∴m=7,
当m=7时,原方程为x2-7x+12=0,
解得,x1=3,x2=4,
不妨设a=3,则sinA=$\frac{a}{c}$=$\frac{3}{5}$,
∴Rt△ABC中较小锐角的正弦值为$\frac{3}{5}$.
故选C.
点评 本题考查了根与系数的关系及锐角三角函数的定义,难度较大,主要掌握利用一元二次方程的根与系数的关系,勾股定理,正弦的概念求解.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
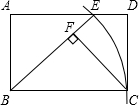 如图,AD∥BC,∠BAD=90°,以点B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过C点作CF⊥BE,垂足为F.
如图,AD∥BC,∠BAD=90°,以点B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过C点作CF⊥BE,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
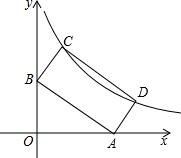 如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.
如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
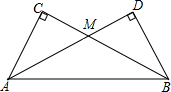 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离.你知道这是为什么吗?
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离.你知道这是为什么吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com