
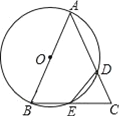
【题目】如图,已知△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于D、E两点,连接ED
(1)求证:△CDE为等腰三角形;
(2)若CD=3,BC=4![]() ,求AD的长和⊙O的半径.
,求AD的长和⊙O的半径.
【答案】(1)详见解析;(2)4.
【解析】
如图,已知△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于D、E两点,连接ED(1)求证:△CDE为等腰三角形;(2)若CD=3,BC=4![]() ,求AD的长和⊙O的半径.
,求AD的长和⊙O的半径.
解:(1)∵∠EDC+∠EDA=180°、∠B+∠EDA=180°,
∴∠B=∠EDC,
又∵AB=AC,
∴∠B=∠C,
∴∠EDC=∠C,
∴ED=EC;
(2)连接AE,
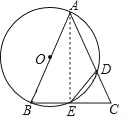
∵AB是直径,
∴AE⊥BC,
又∵AB=AC,
∴BC=2EC=4![]() ,
,
∵∠B=∠EDC、∠C=∠C,
∴△ABC∽△EDC,
∴AB:EC=BC:CD,
又∵CD=3、BC=4![]() ,
,
∴AB:2![]() =4
=4![]() :3,
:3,
∴AB=8,
∴AC=AB=8,AD=AC﹣CD=5,
∴⊙O的半径为4.


科目:初中数学 来源: 题型:
【题目】如图,∴P是菱形ABCD对角线AC上的一点,连接DP并延长DP交边AB于点E,连接BP并延长BP交边AD于点F,交CD的延长线于点G.

(1)求证:△APB≌△APD;
(2)已知DF:FA=1:2,设线段DP的长为x,线段PF的长为y.
①求y与x的函数关系式;
②当x=6时,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是![]() 的中点,CE⊥AB于点E,BD交CE于点F.
的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=5,AC=12,求⊙O的半径和CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
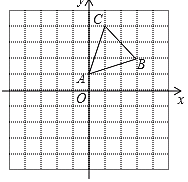
【题目】如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移4个单位得到△A2B2C2,画出△A2B2C2并写出顶点A2,B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
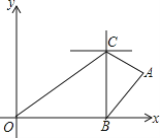
【题目】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为( )

A. 5B. 6C. 8D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为![]() 、
、![]() 、
、![]() ,(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为
,(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为![]() 的圆形区域(只考虑在海平面上的探测).
的圆形区域(只考虑在海平面上的探测).
(1)若在三艘海监船组成的![]() 区域内没有探测盲点,则雷达的有效探测半径
区域内没有探测盲点,则雷达的有效探测半径![]() 至少为________海里;
至少为________海里;
(2)某时刻海面上出现一艘菲律宾海警船![]() ,在海监船
,在海监船![]() 测得点
测得点![]() 位于南偏东
位于南偏东![]() 方向上,同时在海监船
方向上,同时在海监船![]() 测得
测得![]() 位于北偏东
位于北偏东![]() 方向上,海警船
方向上,海警船![]() 正以每小时
正以每小时![]() 海里的速度向正西方向移动,我海监船
海里的速度向正西方向移动,我海监船![]() 立刻向北偏东
立刻向北偏东![]() 方向运动进行拦截,问我海监船
方向运动进行拦截,问我海监船![]() 至少以多少速度才能在此方向上拦截到菲律宾海警船
至少以多少速度才能在此方向上拦截到菲律宾海警船![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com