
【题目】定义:若一个关于x的方程![]() 的解为
的解为![]() ,则称此方程为“中点方程”.如:
,则称此方程为“中点方程”.如:![]() 的解为
的解为![]() ,而
,而![]() ;
;![]() 的解为
的解为![]() ,而
,而![]() .
.
(1)若![]() ,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;
,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;
(2)若关于x的方程![]() 是“中点方程”,求代数式
是“中点方程”,求代数式![]() 的值.
的值.
【答案】(1)不存在;(2)-2019.
【解析】
(1)把![]() 代入原方程解得:x=
代入原方程解得:x=![]() ,若为“中点方程”,则x=
,若为“中点方程”,则x=![]() ,由于b≠b-2,根据“中点方程”定义即可求解;
,由于b≠b-2,根据“中点方程”定义即可求解;
(2)根据“中点方程”定义得到2a2-ab+b=0,![]() =3(2a2-ab+b)-2019,整体代入即可.
=3(2a2-ab+b)-2019,整体代入即可.
解:(1)没有符合要求的“奇异方程”,理由如下:
把![]() 代入原方程解得:x=
代入原方程解得:x=![]() ,
,
若为“中点方程”,则x=![]() ,
,
∵![]() ≠
≠![]() ,
,
∴不符合“中点方程”定义,故不存在;
(2)∵![]() ,
,
∴(2a-b)x+b=0.
∵关于x的方程![]() 是“中点方程”,
是“中点方程”,
∴x=![]() =a.
=a.
把x=a代入原方程得:2a2-ab+b=0,
∴![]() =3(2a2-ab+b)-2019=3
=3(2a2-ab+b)-2019=3![]() 0-2019=-2019.
0-2019=-2019.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
【题目】无锡阳山水蜜桃上市后,甲、乙两超市分别用60000元以相同的进价购进相同箱数的水蜜桃,甲超市销售方案是:将水蜜桃按分类包装销售,其中挑出优质大个的水蜜桃400箱,以进价的2倍价格销售,剩下的水蜜桃以高于进价10%销售.乙超市的销售方案是:不将水蜜桃分类,直接销售,价格按甲超市分类销售的两种水蜜桃售价的平均数定价.若两超市将水蜜桃全部售完,其中甲超市获利42000元(其它成本不计).问:
(1)水蜜桃进价为每箱多少元?
(2)乙超市获利多少元?哪种销售方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2016个正数1、2、3、4…,2016按如图的方式排列成一个表.
(1)如图,用一个正方形框在表中任意框住4个数,记左上角的一个数为x,则另外三个数用含x的式子从小到大依次表示为 , , .
(2)当被框住的4个数的和等于416时,x的值为多少?
(3)能否框住4个数,使它们的和等于324?如能,求出x的值;如不能,请说出理由.
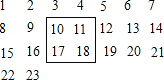
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川苍溪小王家今年红心猕猴桃喜获丰收,采摘上市20天全部销售完,小王对销售情况进行跟踪记录,并将记录情况绘制成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图(1)所示,红星猕猴桃的价格z(单位:元/千克)与上市时间x(天)的函数关系式如图(2)所示.
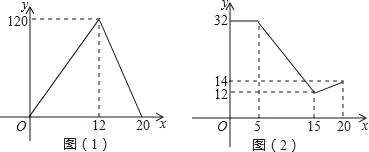
(1)观察图象,直接写出日销售量的最大值;
(2)求小王家红心猕猴桃的日销量y与上市时间x的函数解析式;并写出自变量的取值范围.
(3)试比较第6天和第13天的销售金额哪天多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列货车从北京开往乌鲁木齐,以58km/h的平均速度行驶需要65h.为了实施西部大开发,京乌线决定全线提速.
(1)如果提速后平均速度为vkm/h,全程运营时间为t小时,试写出t与v之间的函数表达式;
(2)如果提速后平均速度为78km/h,求提速后全程运营时间;
(3)如果全程运营的时间控制在40h内,那么提速后,平均速度至少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元。厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;②西装和领带都按定价的90%付款。现某客户要到该服装厂购买西装20套,领带x条(![]() ):
):
(1)若该客户按方案①购买,需付款______________元(用含x的代数式表示);若该客户按方案②购买,需付款________________元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法。
查看答案和解析>>
科目:初中数学 来源: 题型:
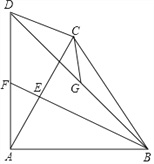
【题目】如图,在四边形ABCD中,![]() ,.连接AC、BD,
,.连接AC、BD,![]() .过点B作
.过点B作![]() ,分别交AC、AD于点E、F.点G为BD中点,连接CG.
,分别交AC、AD于点E、F.点G为BD中点,连接CG.
(1)求证:![]()
(2)根据题中所给条件,猜想:CE与CG的数量关系,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).


请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com