
【题目】四川苍溪小王家今年红心猕猴桃喜获丰收,采摘上市20天全部销售完,小王对销售情况进行跟踪记录,并将记录情况绘制成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图(1)所示,红星猕猴桃的价格z(单位:元/千克)与上市时间x(天)的函数关系式如图(2)所示.
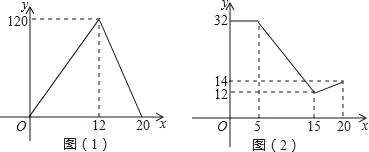
(1)观察图象,直接写出日销售量的最大值;
(2)求小王家红心猕猴桃的日销量y与上市时间x的函数解析式;并写出自变量的取值范围.
(3)试比较第6天和第13天的销售金额哪天多?
【答案】(1)日销售量最大为120千克;(2)![]() ;(3)第6天比第13天销售金额大.
;(3)第6天比第13天销售金额大.
【解析】
(1)观察图(1),可直接得出第12天时,日销售量最大120千克;
(2)观察图(1)可得,日销售量y与上市时间x的函数关系式存在两种形式,根据直线所经过点的坐标,利用待定系数法直接求得函数解析式;
(3)观察图(1),根据(2)求出的函数解析式,分别求出第6天和第13天的日销售量,再根据图(2),求出第6天和第13天的销售单价,求出第6天和第13天的销售金额,最后比较即可.
(1)由图(1)可知,x=12时,日销售量最大,为120千克;
(2)0≤x<12时,设y=k1x,
∵函数图象经过点(12,120),
∴12k1=120,
解得k1=10,
∴y=10x,
12≤x≤20时,设y=k2x+b1,
∵函数图象经过点(12,120),(20,0),
∴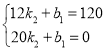 ,
,
解得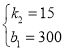 ,
,
∴y=﹣15x+300,
综上所述,y与x的函数关系式为![]() ;
;
(3)5≤x≤15时,设z=k3x+b2,
∵函数图象经过点(5,32),(15,12),
∴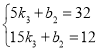 ,
,
解得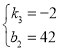 ,
,
∴z=﹣2x+42,
x=6时,y=60,z=﹣2×6+42=30,
∴销售金额=60×30=1800元,
x=13时,y=﹣15×13+300=105,
z=﹣2×13+42=16,
∴销售金额=105×16=1680元,
∵1800>1680,
∴第6天比第13天销售金额大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知,点A、B、O在数轴上对应的数为a、b、0,且满足|a+8|+(b﹣12)2=0,点M、N分别从O、B出发,同时向左匀速运动,M的速度为1个单位长度每秒,N的速度为3个单位长度每秒,A、B之间的距离定义为:AB=|a﹣b|.
(1)直接写出OA= .OB= ;
(2)设运动的时间为t秒,当t为何值时,恰好有AN=2AM;
(3)若点P为线段AM的中点,Q为线段BN的中点,M、N在运动的过程中,PQ+MN的长度是否发生变化?若不变,请说明理由,若变化,当t为何值时,PQ+MN有最小值?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业投资112万元引进一条农产品加工生产线,若不计维修、保养等费用,预计投产后每年可创利33万元,该生产线投产后从第一年到第x年的维修、保养费用累计为y万元,且y=ax 2 +bx,若第一年的维修保养费用为2万元,第二年为4万元.
(1)求y关于x的解析式;
(2)设x年后企业纯利润为z万元(纯利润=创利-维修、保养费用),投产后这个企业在第几年就能收回投资?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别把带有指针的圆形转盘A、B分成4等份、3等份的扇形区域,并在每一个小区域内标上数字(如图所示).欢欢、乐乐两个人玩转盘游戏,游戏规则是:同时转动两个转盘,当转盘停止时,若指针所指两区域的数字之积为奇数,则欢欢胜;若指针所指两区域的数字之积为偶数,则乐乐胜;若有指针落在分割线上,则无效,需重新转动转盘.
(1)试用列表或画树状图的方法,求欢欢获胜的概率;
(2)请问这个游戏规则对欢欢、乐乐双方公平吗?试说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式,你发现了什么规律?
12=![]() ;12+22=
;12+22=![]() ;12+22+32 =
;12+22+32 =![]() ; 12+22 +32 + 42 =
; 12+22 +32 + 42 =![]() ;…
;…
1)你能用一个算式表示这个规律吗?
2)根据你发现的规律,计算下面算式的值;
12+22 +32 + … +82
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是________(填A或B或C)
A.a2-2ab+b2=(a-b)2
B.a2-b2=(a+b)(a-b)
C.a2+ab=a(a+b)
(2)应用你从(1)中选出的等式,完成下列各题:
①已知x2-4y2=12,x+2y=4,求x-2y的值
②计算:(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )…(1-
)…(1-![]() )(1-
)(1-![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一个关于x的方程![]() 的解为
的解为![]() ,则称此方程为“中点方程”.如:
,则称此方程为“中点方程”.如:![]() 的解为
的解为![]() ,而
,而![]() ;
;![]() 的解为
的解为![]() ,而
,而![]() .
.
(1)若![]() ,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;
,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;
(2)若关于x的方程![]() 是“中点方程”,求代数式
是“中点方程”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线y=![]() (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
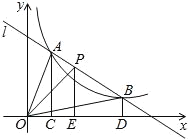
A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A和B.
轴分别相交于点A和B.
(1)直接写出坐标:点A ,点B ;
(2)以线段AB为一边在第一象限内作□ABCD,其顶点D(![]() ,
, ![]() )在双曲线
)在双曲线![]() (
(![]() >
>![]() )上.
)上.
①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿![]() 轴向左平移多少个单位长度时,点C恰好落在双曲线
轴向左平移多少个单位长度时,点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com