
【题目】如图,在四边形ABCD中,![]() ,.连接AC、BD,
,.连接AC、BD,![]() .过点B作
.过点B作![]() ,分别交AC、AD于点E、F.点G为BD中点,连接CG.
,分别交AC、AD于点E、F.点G为BD中点,连接CG.
(1)求证:![]()
(2)根据题中所给条件,猜想:CE与CG的数量关系,并请说明理由.
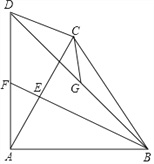
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)根据AB⊥AD,BE⊥AC,可推导得出∠ABE=∠DAC,再根据∠DCA=∠AEB=90°,AB=AD,即可得△ABE≌△DAC;
(2)结论:CE=![]() CG,连接AG、EG,证明△CAG≌△EBG,从而得到CG=EG,∠ACG=∠BEG,
CG,连接AG、EG,证明△CAG≌△EBG,从而得到CG=EG,∠ACG=∠BEG,
继而可得∠ACG=∠CEG=∠GEB,再根据BE⊥AC,从而得∠ACG=∠CEG=∠GEB=45°,得到∠CGE=90°,得到CE=![]() CG.
CG.
试题解析:(1)∵AB⊥AD,∴∠BAE+∠DAC=90°,
又∵BE⊥AC,∴∠BAE+∠ABE=90°,
∴∠ABE=∠DAC,
∵AC⊥DC,∴∠DCA=∠AEB=90°,
又∵AB=AD,∴△ABE≌△DAC;
(2)结论:CE=![]() CG,理由如下:
CG,理由如下:
连接AG、EG,
由(1)知BE=AC,∠DAC=∠ABE,
∵∠BAD=90°,AB=AD,G为BD的中点,∴AG=BG,∠DAG=∠BAG=∠ABD=45°,
∵∠DAC=∠ABE,∴∠CAG=∠EBG,
又∵BE=AC,AG=BG,∴△CAG≌△EBG,
∴CG=EG,∠ACG=∠BEG,
∴∠ACG=∠CEG,∴∠ACG=∠CEG=∠GEB,
又∵BE⊥AC,∴∠ACG=∠CEG=∠GEB=45°,
∴∠CGE=90°,∴CE=![]() CG.
CG.


科目:初中数学 来源: 题型:
【题目】某企业投资112万元引进一条农产品加工生产线,若不计维修、保养等费用,预计投产后每年可创利33万元,该生产线投产后从第一年到第x年的维修、保养费用累计为y万元,且y=ax 2 +bx,若第一年的维修保养费用为2万元,第二年为4万元.
(1)求y关于x的解析式;
(2)设x年后企业纯利润为z万元(纯利润=创利-维修、保养费用),投产后这个企业在第几年就能收回投资?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一个关于x的方程![]() 的解为
的解为![]() ,则称此方程为“中点方程”.如:
,则称此方程为“中点方程”.如:![]() 的解为
的解为![]() ,而
,而![]() ;
;![]() 的解为
的解为![]() ,而
,而![]() .
.
(1)若![]() ,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;
,有符合要求的“中点方程”吗?若有,请求出该方程的解;若没有请说明理由;
(2)若关于x的方程![]() 是“中点方程”,求代数式
是“中点方程”,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线y=![]() (k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则( )
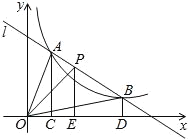
A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
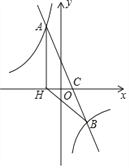
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数![]() 的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=
的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=![]() ,tan∠ACH=2,且点B的坐标为(4,n).
,tan∠ACH=2,且点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上原点左边有一点A,点A对应着数a,有如下说法:
①﹣a表示的数一定是一个正数.
②若|a|=9时,则a=﹣9.
③在﹣a,![]() ,a2,a3中,最大的数值是a2.
,a2,a3中,最大的数值是a2.
④式子|a+![]() |的最小值为2.
|的最小值为2.
其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E

(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A和B.
轴分别相交于点A和B.
(1)直接写出坐标:点A ,点B ;
(2)以线段AB为一边在第一象限内作□ABCD,其顶点D(![]() ,
, ![]() )在双曲线
)在双曲线![]() (
(![]() >
>![]() )上.
)上.
①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿![]() 轴向左平移多少个单位长度时,点C恰好落在双曲线
轴向左平移多少个单位长度时,点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且|a|=|c|.
(1)若|a+c|+|b|=2,求b的值;
(2)用“>”从大到小把a,b,﹣b,c连接起来.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com