
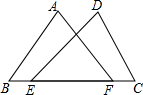
 如图,点E,F在BC边上,AB=DC,∠B=∠C.要使得∠A=∠D.则可以添加的条件是∠AFE=∠DEF或BF=CE或BE=CF(答案不唯一)(写一个即可).
如图,点E,F在BC边上,AB=DC,∠B=∠C.要使得∠A=∠D.则可以添加的条件是∠AFE=∠DEF或BF=CE或BE=CF(答案不唯一)(写一个即可). 科目:初中数学 来源: 题型:填空题
 如图,点D是△ABC的边BC上的一点,则在△ABC中∠C所对的边是AB;在△ACD中∠C所对的边是AD;在△ABD中边AD所对的角是∠B;在△ACD中边AD所对的角是∠C.
如图,点D是△ABC的边BC上的一点,则在△ABC中∠C所对的边是AB;在△ACD中∠C所对的边是AD;在△ABD中边AD所对的角是∠B;在△ACD中边AD所对的角是∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.
小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用如图所示形状的甲、乙两个框,都能框住某月日历表中的四个数,设被框住的四个数中:甲框住的最小的数为a;乙框住的最小的数为b.
用如图所示形状的甲、乙两个框,都能框住某月日历表中的四个数,设被框住的四个数中:甲框住的最小的数为a;乙框住的最小的数为b.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系内,已知点A(0,6),点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
在平面直角坐标系内,已知点A(0,6),点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com