

分析 (1)利用三角函数求出线段CD,延长AD交EF于点H,利用三角函数即可求出线段DH长度,再除以运动速度即为运动时间;
(2)分五种情况进行讨论,求出重合面积,写出S关于t的函数关系式即可;
(3)通过分析△C1PQ为等腰三角形,分析等腰情况,分别求出对应角度即可.
解答 解:(1)∵AD=BC=6,∠ACB=30°,
∴AB=DF=6×tan30°=2$\sqrt{3}$,
延长AD交EF于点H,如下图:
∵△ACD绕点C顺时针旋转得到△EFG,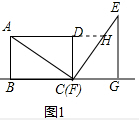
∴∠DFH=30°,
∴DH=DF×tan30°=2,
∵△EFG以每秒1个单位长度的速度沿直线CB向左平移,2÷1=2秒,
∴当t=2时,点D落在线段EF上.
(2)当0<t≤2时,S=$\frac{\sqrt{3}}{2}$t2,
当2<t≤2$\sqrt{3}$时,S=2$\sqrt{3}$t-2$\sqrt{3}$,
当2$\sqrt{3}$<t≤6时,S=12-2$\sqrt{3}$,
当6<t≤8时,S=-$\frac{\sqrt{3}}{2}$t2+6$\sqrt{3}$t-20$\sqrt{3}$+12,
当8<t<6+2$\sqrt{3}$时,S=-2$\sqrt{3}$t+12$\sqrt{3}$+12,
(3)30°、120°、165°.
∵△C1PQ为等腰三角形,
当PQ=PC′,如下图: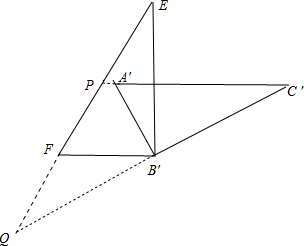
则∠Q=∠C′=30°,
∴∠EPC′=60°,
∵∠E=30°,
∴∠A′B′E=30°,
∴α=30°.
同理:当PQ=QC′,PC′=QC′,α=120°、165°.
∴△C1PQ为等腰三角形,旋转角为30°、120°、165°.
点评 题目考查了几何图形的综合变换,解决此类问题的关键分析图形的变换情况,在变换过程中,分析变量和不变量,题目整体较难,适合学生压轴训练.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
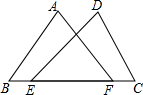 如图,点E,F在BC边上,AB=DC,∠B=∠C.要使得∠A=∠D.则可以添加的条件是∠AFE=∠DEF或BF=CE或BE=CF(答案不唯一)(写一个即可).
如图,点E,F在BC边上,AB=DC,∠B=∠C.要使得∠A=∠D.则可以添加的条件是∠AFE=∠DEF或BF=CE或BE=CF(答案不唯一)(写一个即可).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形是正方形,BM=DF,AF垂直AM,点M、B、C在一条直线上,且△AEM与△AEF恰好关于所在直线成轴对称.已知EF=x,正方形边长为y.
如图,四边形是正方形,BM=DF,AF垂直AM,点M、B、C在一条直线上,且△AEM与△AEF恰好关于所在直线成轴对称.已知EF=x,正方形边长为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图所示,点D、E分别在等边△ABC的边BC、AC上,且AE=CD,AD与BE相交于点F.
已知:如图所示,点D、E分别在等边△ABC的边BC、AC上,且AE=CD,AD与BE相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com