
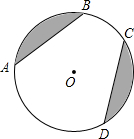
 如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,弦AB长为8,DC长为4,则S阴影为10π-16.
如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,弦AB长为8,DC长为4,则S阴影为10π-16. 分析 此题若直接求阴影部分的面积,缺少必要的条件如:圆的半径、两个扇形圆心角的度数等,如果将两个图形进行适当变形,解题方法就会简便许多.令B、C重合,根据已知的弧的等量关系,可判定此时AD为⊙O的直径,那么阴影部分的面积即为半圆的面积和Rt△ADC的面积差,由此得解.
解答 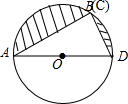 解:如图,令B、C重合;
解:如图,令B、C重合;
∵$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,
∴AD是⊙O的直径;
在Rt△ABD中,AB=8,AD=4,由勾股定理得:
BD2=AB2+AD2=80,
故S阴影=S半圆-S△ABD=$\frac{1}{2}$×π×($\frac{1}{2}$AD)2-$\frac{1}{2}$×8×4=10π-16.
故答案为:10π-16.
点评 本题考查了扇形面积的计算,能够对图形进行合理的变形或整理是解决此题的关键.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:填空题
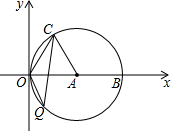 如图,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,当点P在直径OB上运动时,连CP并延长与⊙A相交于点Q,PO=2或2+2$\sqrt{3}$时,△OCQ是等腰三角形.
如图,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,当点P在直径OB上运动时,连CP并延长与⊙A相交于点Q,PO=2或2+2$\sqrt{3}$时,△OCQ是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
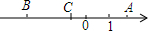 有理数a、b、c在数轴上对应的点分别是A、B、C,其位置如图所示.试化简:
有理数a、b、c在数轴上对应的点分别是A、B、C,其位置如图所示.试化简:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com