
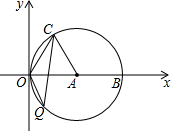
 如图,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,当点P在直径OB上运动时,连CP并延长与⊙A相交于点Q,PO=2或2+2$\sqrt{3}$时,△OCQ是等腰三角形.
如图,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,当点P在直径OB上运动时,连CP并延长与⊙A相交于点Q,PO=2或2+2$\sqrt{3}$时,△OCQ是等腰三角形. 分析 本题分两种情况:
①以O为顶点,OC,OQ为腰.那么可过C作x轴的垂线,交圆于Q,此时三角形OCQ就是此类情况所说的等腰三角形;那么此时PO可在直角三角形OCP中,根据∠COA的度数,和OC即半径的长求出PO.
②以Q为顶点,QC,QD为腰,那么可做OC的垂直平分线交圆于Q,则这条线必过圆心,如果设垂直平分线交OC于D的话,可在直角三角形AOQ中根据∠QAE的度数和半径的长求出Q的坐标;然后用待定系数法求出CQ所在直线的解析式,得出这条直线与x轴的交点,也就求出了PO的值.
解答 解:①过点C作CP1⊥OB,垂足为P1,延长CP1交⊙A于Q1;如图①,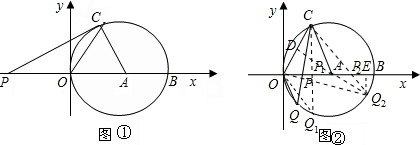
∵OA是半径,
∴$\widehat{OC}=\widehat{O{Q}_{1}}$,
∴OC=OQ1,
∴△OCQ1是等腰三角形;
又∵△AOC是等边三角形,
∴P1O=$\frac{1}{2}$OA=2;
②过A作AD⊥OC,垂足为D,延长DA交⊙A于Q2,CQ2与x轴交于P2;如图②,
∵A是圆心,
∴DQ2是OC的垂直平分线,
∴CQ2=OQ2,
∴△OCQ2是等腰三角形;
过点Q2作Q2E⊥x轴于E,
在Rt△AQ2E中,
∵∠Q2AE=∠OAD=$\frac{1}{2}$∠OAC=30°,
∴Q2E=$\frac{1}{2}$AQ2=2,AE=2$\sqrt{3}$,
∴点Q2的坐标(4+$2\sqrt{3}$,-2);
在Rt△COP1中,
∵P1O=2,∠AOC=60°,
∴$C{P}_{1}=2\sqrt{3}$
∴C点坐标(2,$2\sqrt{3}$);
设直线CQ2的关系式为y=kx+b,则
$\left\{\begin{array}{l}{-2=(4+2\sqrt{3})k+b}\\{2\sqrt{3}=2k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=2+2\sqrt{3}}\end{array}\right.$,
∴y=-x+2+2$\sqrt{3}$;
当y=0时,x=2+2$\sqrt{3}$,
∴P2O=2+2$\sqrt{3}$.
故答案为:2或2+2$\sqrt{3}$.
点评 本题综合考查函数、圆的切线,等边三角形的判定以及垂径定理等知识点.要注意等腰三角形要按顶点和腰的不同来分类讨论.


科目:初中数学 来源: 题型:解答题
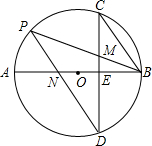 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当x≥2时,y随x增大而增大 | B. | 对称轴为直线x=3 | ||
| C. | 当x=3时,y有最小值2 | D. | 顶点坐标为(3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
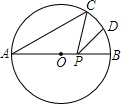 如图,AB是⊙O的直径,AB=4,点C在⊙O上,∠CAB=30°,D为$\widehat{BC}$的中点,P是直径AB上一动点,则PC+PD的最小值为( )
如图,AB是⊙O的直径,AB=4,点C在⊙O上,∠CAB=30°,D为$\widehat{BC}$的中点,P是直径AB上一动点,则PC+PD的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.8(1+x)=5 | B. | 1.8(1+2x)=5 | ||
| C. | 1.8(1+x)2=5 | D. | 1.8(1+x)+1.8(1+x)2=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
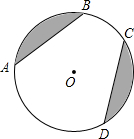 如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,弦AB长为8,DC长为4,则S阴影为10π-16.
如图,$\widehat{AB}$+$\widehat{CD}$=$\widehat{AD}$+$\widehat{BC}$,弦AB长为8,DC长为4,则S阴影为10π-16.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com