
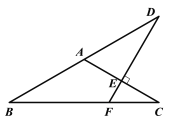
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,线段AC的垂直平分线交BC于点F,交AC于点E,交BA的延长线于点D.若DE=3,则BF=( ).
A.4B.3C.2D.![]()
【答案】A
【解析】
连接AF,利用等腰三角形的性质得到∠B=∠C=30°,则∠BAF=90°,再根据线段垂直平分线的性质得到FA=FC,则∠FAC=∠C=30°,然后在Rt△AED中就是出AE=![]() ,在Rt△AEF中就是出EF=
,在Rt△AEF中就是出EF=![]() AE=1,AF=2EF=2,最后在Rt△ABF中就是出BF.
AE=1,AF=2EF=2,最后在Rt△ABF中就是出BF.
连接AF,如图,

∵AB=AC,∠BAC=120°.
∴∠B=∠C=30°,
∵ED垂直平分AC,
∴FA=FC,
∴∠FAC=∠C=30°,
∴∠AFD=60°,∠D=30°,
∴∠BAF=90°,
在Rt△AED中,AE=![]() ED=
ED=![]() ,
,
在Rt△AEF中,EF=![]() AE=1,AF=2EF=2,
AE=1,AF=2EF=2,
在Rt△ABF中,BF=2AF=4.
故选:A.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】△ABC内接于⊙O,AB=AC,BD⊥AC,垂足为点D,交⊙O于点E,连接AE.
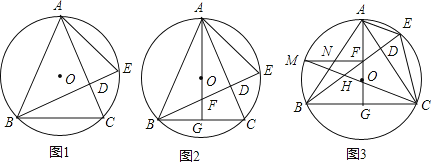
(1)如图1,求证:∠BAC=2∠CAE;
(2)如图2,射线AO交线段BD于点F,交BC边于点G,连接CE,求证:BF=CE;
(3)如图3,在(2)的条件下,连接CO并延长,交线段BD于点H,交⊙O于点M,连接FM,交AB边于点N,若BH=DH,四边形BHOG的面积为5![]() ,求线段MN的长.
,求线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△AOB中,∠AOB=90°,∠ABO=30°,顶点A在反比例函y=![]() (x>0)上运动,此时顶点B也在反比例函数y=
(x>0)上运动,此时顶点B也在反比例函数y=![]() 上运动,则m的值为( )
上运动,则m的值为( )
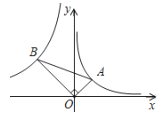
A.-9B.-12C.-15D.-18
查看答案和解析>>
科目:初中数学 来源: 题型:
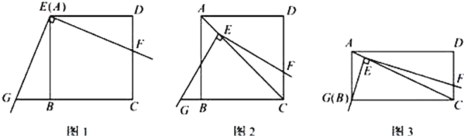
【题目】如图1,将三角板放在正方形![]() 上,使三角板的直角顶点
上,使三角板的直角顶点![]() 与正方形
与正方形![]() 的顶点
的顶点![]() 重合,三角板的一边交
重合,三角板的一边交![]() 于点
于点![]() .另一边交
.另一边交![]() 的延长线于点
的延长线于点![]() .
.
(1)观察猜想:线段![]() 与线段
与线段![]() 的数量关系是_____;
的数量关系是_____;
(2)探究证明:如图2,移动三角板,使顶点![]() 始终在正方形
始终在正方形![]() 的对角线
的对角线![]() 上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)拓展延伸:如图3,将(2)中的“正方形![]() ”改为“矩形
”改为“矩形![]() ”,且使三角板的一边经过点
”,且使三角板的一边经过点![]() ,其他条件不变,若
,其他条件不变,若![]() 、
、![]() ,请探究线段
,请探究线段![]() 与线段
与线段![]() 之间存在怎样的数量关系?(用含
之间存在怎样的数量关系?(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面贯彻党的教育方针,坚持“健康第一”的教育理念,促进学生健康成长,提高体质健康水平,成都市调整体育中考实施方案:分值增加至60,男1000米(女800米)必考,足球、篮球、排球“三选一”…,从2019年秋季新入学的七年级起开始实施.某中学为了解七年级学生对三大球类运动的喜爱情况,从七年级学生中随机抽取部分学生进行调查问卷,通过分析整理绘制了如下两幅统计图.请根据两幅统计图中的信息回答下列问题:
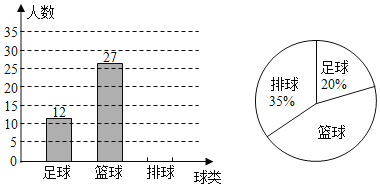
(1)求参与调查的学生中,喜爱排球运动的学生人数,并补全条形图;
(2)若该中学七年级共有400名学生,请你估计该中学七年级学生中喜爱篮球运动的学生有多少名?
(3)若从喜爱足球运动的2名男生和2名女生中随机抽取2名学生,确定为该校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F.
(1)求证:DF是⊙O的切线;
(2)过点F作FG⊥AB,垂足为G,若AB=12.
①求FG的长;
②求点D到FG的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
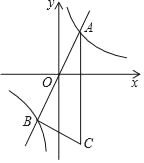
【题目】如图,反比例函数的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,CA∥y轴,∠ABC=90°
(1)求反比例函数的解析式及点B的坐标;
(2)求tanC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,边长为8,E是AB边上的一点,连接DE,将△DAE沿DE所在直线折叠,使点A的对应点A1落在正方形的边CD或BC的垂直平分线上,则AE的长度是_____.
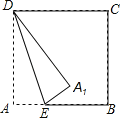
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=8,BC=6,点E,F分别为AB,AD边上任意一点,现将△AEF沿直线EF对折,点A对应点为点G.
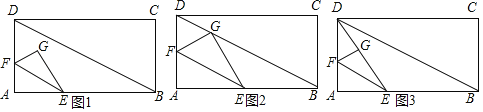
(1)如图2,当EF∥BD,且点G落在对角线BD上时,求DG的长;
(2)如图3,连接DG,当EF∥BD且△DFG是直角三角形时,求AE的值;
(3)当AE=2AF时,FG的延长线交△BCD的边于点H,是否存在一点H,使得以E,H,G为顶点的三角形与△AEF相似,若存在,请求出AE的值;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com