
【题目】如图1,矩形ABCD中,AB=8,BC=6,点E,F分别为AB,AD边上任意一点,现将△AEF沿直线EF对折,点A对应点为点G.
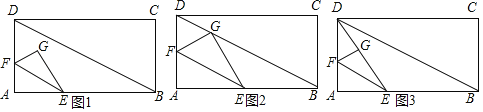
(1)如图2,当EF∥BD,且点G落在对角线BD上时,求DG的长;
(2)如图3,连接DG,当EF∥BD且△DFG是直角三角形时,求AE的值;
(3)当AE=2AF时,FG的延长线交△BCD的边于点H,是否存在一点H,使得以E,H,G为顶点的三角形与△AEF相似,若存在,请求出AE的值;若不存在,请说明理由
【答案】(1)![]() ;(2)AE=
;(2)AE=![]() 或
或![]() ;(3)存在,满足条件的AE的值为3或
;(3)存在,满足条件的AE的值为3或![]() 或
或![]() 或
或![]()
【解析】
(1)连接AG,如图2所示,首先证明AG⊥BD,解直角三角形即可解决问题;
(2)分两种情形:①当∠DGF=90°时,此时点D,G,E三点共线,②当∠GDF=90°时,点G在DC上,过点E作EH⊥CD于H,则四边形ADHE是矩形,分别求解即可;
(3)分四种情形:①当△AEF∽△GHE时,如图4﹣1,过点H作HP⊥AB于P;②当△AEF∽△GHE时,如图4﹣2,过点H作HP⊥AB于P;③当△AEF∽△GEH时,如图4﹣3,过点G作MN∥AB交AD于点M,过点E作EN⊥MN于N;④当△AEF∽△GEH时,如图4﹣4,过点G作MN∥AB交AD于点M,过点E作EN⊥MN于N,过点H作HQ⊥AD于Q,分别求解即可.
解:(1)连接AG,如图2所示,
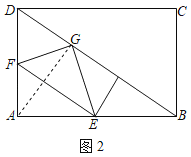
由折叠得:AG⊥EF,
∵EF∥BD,
∴AG⊥BD,
在矩形ABCD中,AB=8,BC=6,
∴∠DAB=90°,AD=BC=6,
∴DB=![]() =
=![]() =10,
=10,
∴cos∠ADB=![]() =
=![]() =
=![]() ,
,
∴DG=ADcos∠ADB=6×![]() =
=![]() ;
;
(2)①当∠DGF=90°时,此时点D,G,E三点共线,

设AF=3t,则FG=3t,AE=4t,DF=6﹣3t,
在Rt△DFG中,DG2+FG2=DF2,即DG2=(6﹣3t)2﹣(3t)2=36﹣36t,
∵tan∠FDG=![]() =
=![]() ,
,
∴![]() ,
,
解得t=![]() ,
,
∴AE=![]() ;
;
②当∠GDF=90°时,点G在DC上,过点E作EH⊥CD于H,则四边形ADHE是矩形,EH=AD=6.
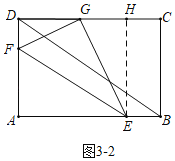
设AF=3t,则FG=3t,AE=4t,DF=6﹣3t,
∵∠FDG=∠FGE=∠EHG=90°,
∴∠DGF+∠DFG=90°,∠DGF+∠EGH=90°,
∴∠DFG=∠EGH,
∴△GDF∽△EHG,
∴![]() ,
,
∴![]() ,
,
∴DG=![]() ,GH=8﹣4k,
,GH=8﹣4k,
∵DG+GH=AE,
∴![]() +8﹣4k=4k,
+8﹣4k=4k,
∴k=![]() ,
,
∴AE=![]() ,
,
综上所述:AE=![]() 或
或![]() ;
;
(3)①当△AEF∽△GHE时,如图4﹣1,过点H作HP⊥AB于P,
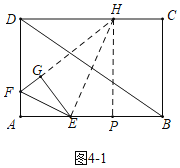
∵∠AEF=∠FEG=∠EHG,∠EHG+∠HEG=90°,
∴△FEG+∠HEG=90°,
∴∠A=∠FEH=90°,
∴△AEF∽△EHF,
∴EF:HE=AF:AE=1:2,
∵∠A=∠HPE=90°,
∴∠AEF+∠HEP=90°,∠HEP+∠EHP=90°,
∴∠AEF=∠EHP,
∴△AEF∽△HPE,
∴EA:HP=EF:EH=1:2,
∵HP=6,
∴AE=3;
②当△AEF∽△GHE时,如图4﹣2,过点H作HP⊥AB于P,

同法可得EF:HE=1:2,EA:HP=1:2,
设AF=t,则AE=2t,EP=2t,HP=4t,
∴BP=8﹣4t,
∵△BHP∽△BDA,
∴4t:6=(8﹣4t):8,
解得:t=![]() ,AE=
,AE=![]() ;
;
③当△AEF∽△GEH时,如图4﹣3,过点G作MN∥AB交AD于点M,过点E作EN⊥MN于N.

设AF=t,则AE=2t,DF=6﹣t,
由翻折可知:△AEF≌△GEF,AE=GE,
∵△AEF∽△GEH,AE=GE,
∴△AEF≌△GEH(AAS或ASA),
∴FG=GH,
∵MG∥DH,
∴FM=![]() (6﹣t),
(6﹣t),
∴AM=EN=AF+FM=![]() ,
,
又∵△FMG∽△GNE,且GF:GE=1:2,
∵MG=![]() NE=
NE=![]() AM=
AM=![]() ,GN=2FN=6﹣t,
,GN=2FN=6﹣t,
∵MN=AE,
∴![]() +6﹣t=2t,
+6﹣t=2t,
解得t=![]() ,
,
∴AE=![]() ;
;
④当△AEF∽△GEH时,如图4﹣4,过点G作MN∥AB交AD于点M,过点E作EN⊥MN于N,过点H作HQ⊥AD于Q,设AF=t,则AE=2t,
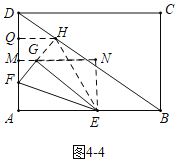
设FM=a,
∴NG=2a,NE=a+t,
∴MG=![]() EN=
EN=![]() AM=
AM=![]() ,
,
∴![]() +2a=2t①,
+2a=2t①,
由上题可知:MF=MQ=a,QH=2MG=a+t,
∴DQ=6﹣t﹣2a,
∵![]() ,
,
∴![]() ②,
②,
解得t=![]() ,
,
∴AE=![]() ,
,
综上所述,满足条件的AE的值为3或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,线段AC的垂直平分线交BC于点F,交AC于点E,交BA的延长线于点D.若DE=3,则BF=( ).
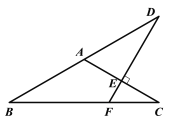
A.4B.3C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织全校学生进行了一次“社会主义核心价值观”知识竞赛,赛后随机抽取了各年级部分学生成绩进行统计,制作如下频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段( | 频数 | 频率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
(1)请求出该校随机抽取了____学生成绩进行统计;
(2)表中![]() ____,
____,![]() ____,并补全直方图;
____,并补全直方图;
(3)若用扇形统计图描述此成绩统计分布情况,则分数段![]() 对应扇形的圆心角度数是___
对应扇形的圆心角度数是___![]() ;
;
(4)若该校共有学生8000人,请估计该校分数在![]() 的学生有多少人?
的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
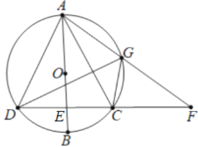
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E ,G是弧AC上的点,AG,DC延长线交于点F.
(1)求证:∠FGC=∠AGD.
(2)若BE=2,CD=8,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种推磨工具模型,图2是它的示意图,已知AB⊥PQ,AP=AQ=3dm,AB=12dm,点A在中轴线l上运动,点B在以O为圆心,OB长为半径的圆上运动,且OB=4dm.
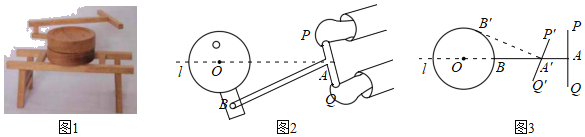
(1)如图3,当点B按逆时针方向运动到B′时,A′B′与⊙O相切,则AA′=__dm.
(2)在点B的运动过程中,点P与点O之间的最短距离为__dm.
查看答案和解析>>
科目:初中数学 来源: 题型:
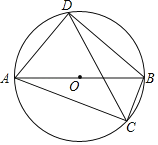
【题目】如图,AB是⊙O的直径,AC、BC是⊙O的弦,∠ACB的平分线交⊙O于D,连接AD、BD,已知AB=6,BC=2.
(1)求AD的长度和四边形ACBD的面积;
(2)证明:2AD2=AC2+BC2.
查看答案和解析>>
科目:初中数学 来源: 题型:
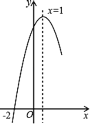
【题目】抛物线![]() 经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
①![]() ;
;
②![]() >
>![]() ;
;
③若n>m>0,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值;
时的函数值;
④点(![]() ,0)一定在此抛物线上.
,0)一定在此抛物线上.
其中正确结论的个数是( )
A.4个B.3个
C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
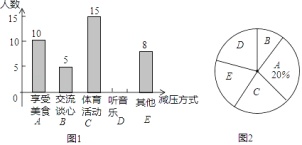
![]() 九年级接受调查的同学共有多少名,并补全条形统计图;
九年级接受调查的同学共有多少名,并补全条形统计图;
![]() 九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
![]() 若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com