
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践及创客空间,致力于从小培养学生的创新精神和创造能力,某校开设了“3D”打印,数学编程,智能机器人,陶艺制作,这四门创客课程,为了了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查,将调查结果整理后绘制成如下的统计图表:
创客课程 | 频数 | 频率 |
“3D”打印 | 36 | 0.45 |
数学编程 | 0.25 | |
智能机器人 | 16 | b |
陶艺制作 | 8 | |
合计 | a | 1 |

根据图表中提供的信息回答下列问题:
(1)统计表中的a=________,b=________;
(2)“陶艺制作”对应扇形的圆心角度数为________;
(3)若该校有学生2000人,请估算全校喜爱“智能机器人”的人数有多少?
科目:初中数学 来源: 题型:
【题目】A市准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的提示牌和垃圾箱,若购买2个提示牌和3个垃圾箱共需550元,且垃圾箱的单价是提示牌单价的3倍.
(1)求提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开.某茶店用4000元购进了A种茶叶若干盒,用8400元购进B种茶叶若干盒,所购B种茶叶比A种茶叶多10盒,且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍.
(1)A,B两种茶叶每盒进价分别为多少元?
(2)第一次所购茶叶全部售完后第二次购进A,B两种茶叶共100盒(进价不变),A种茶叶的售价是每盒300元,B种茶叶的售价是每盒400元.两种茶叶各售出一半后,为庆祝国际茶日,两种茶叶均打七折销售,全部售出后,第二次所购茶叶的利润为5800元(不考虑其他因素),求本次购进A,B两种茶叶各多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
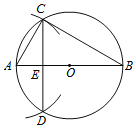
【题目】已知⊙O.如图,
(1)作⊙O的直径AB;
(2)以点A为圆心,AO长为半径画弧,交⊙O于C,D两点;
(3)连接CD交AB于点E,连接AC,BC.
根据以上作图过程及所作图形,有下面三个推断:
①CE=DE; ②BE=3AE; ③BC=2CE.
所有正确推断的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的函数解析式为
的函数解析式为![]() ,若抛物线
,若抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() .
.
(1)求抛物线![]() 的解析式.
的解析式.
(2)已知实数![]() ,请证明:
,请证明:![]() ,并说明
,并说明![]() 为何值时才会有
为何值时才会有![]() .
.
(3)若抛物线![]() 先向上平移4个单位,再向左平移1个单位后得到抛物线
先向上平移4个单位,再向左平移1个单位后得到抛物线![]() ,设
,设![]() ,
,![]() 是
是![]() 上的两个不同点,且满足:
上的两个不同点,且满足:![]() ,
,![]() ,
,![]() .请你用含有
.请你用含有![]() 的表达式表示出
的表达式表示出![]() 的面积
的面积![]() ,并求出
,并求出![]() 的最小值及
的最小值及![]() 取最小值时一次函数
取最小值时一次函数![]() 的函数解析式.
的函数解析式.
(参考公式:在平面直角坐标系中,若![]() ,则
,则![]() 两点间的距离
两点间的距离![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药,12周后,记录了两组患者的生理指标![]() 和
和![]() 的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
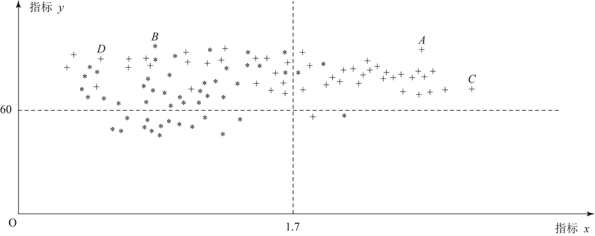
同时记录了服药患者在4周、8周、12周后的指标z的改善情况,并绘制成条形统计图.

根据以上信息,回答下列问题:
(1)从服药的50名患者中随机选出一人,求此人指标![]() 的值大于1.7的概率;
的值大于1.7的概率;
(2)设这100名患者中服药者指标![]() 数据的方差为
数据的方差为![]() ,未服药者指标
,未服药者指标![]() 数据的方差为
数据的方差为![]() ,则
,则![]()
![]() ;(填“>”、“=”或“<” )
;(填“>”、“=”或“<” )
(3)对于指标z的改善情况,下列推断合理的是 .
①服药4周后,超过一半的患者指标z没有改善,说明此药对指标z没有太大作用;
②在服药的12周内,随着服药时间的增长,对指标z的改善效果越来越明显.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数![]() 的图象如图,现给出下列结论:①
的图象如图,现给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 的两个根为
的两个根为![]() ,
,![]() ,其中正确的结论有( )
,其中正确的结论有( )
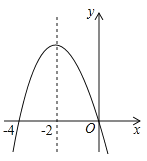
A.①③④B.②④⑤C.①②⑤D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
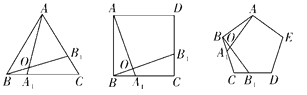
【题目】如图,下列正多边形都满足BA1=CB1,在正三角形中,我们可推得:∠AOB1=60°;在正方形中,可推得:∠AOB1=90°;在正五边形中,可推得:∠AOB1=108°,依此类推在正八边形中,AOB1=____°,在正n(n≥3)边形中,∠AOB1=____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
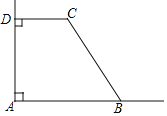
【题目】如图所示,AB⊥AD于点A,CD⊥AD于点D,∠C=120°.若线段BC与CD的和为12,则四边形ABCD的面积可能是( )
A.24![]() B.30
B.30![]() C.45D.
C.45D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com