
【题目】如图①,正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上(不与点
上(不与点![]() ,
,![]() 重合)的一个动点,过点
重合)的一个动点,过点![]() 作
作![]() 且
且![]() 交边
交边![]() 于点
于点![]() .
.
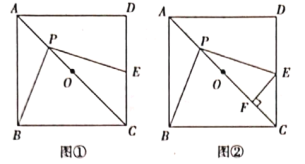
(1)求证:![]() .
.
(2)如图②,若正方形![]() 的边长为
的边长为![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,在点
,在点![]() 运动的过程中,
运动的过程中,![]() 的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由.
的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由.
(3)用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1)见解析;(2)在![]() 点运动的过程中,
点运动的过程中,![]() 的长度不发生变化,理由见解析;(3)
的长度不发生变化,理由见解析;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)作辅助线,构建全等三角形,根据ASA证明△BMP≌△PNE可得结论;
(2)如图②,连接OB,通过证明△OBP≌△FPE,得PF=OB,则PF为定值是![]() ;
;
(3)根据△AMP和△PCN是等腰直角三角形,得PA=![]() PM,PC=
PM,PC=![]() NC,整理可得结论.
NC,整理可得结论.
(1)证明:如图①,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
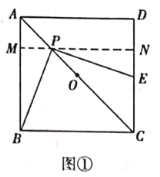
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵四边形![]() 是正方形,
是正方形,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)解:在![]() 点运动的过程中,
点运动的过程中,![]() 的长度不发生变化.
的长度不发生变化.
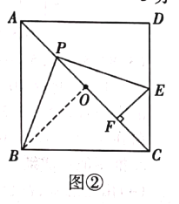
理由:如图②,连接![]() .
.
∵点![]() 是正方形
是正方形![]() 对角线
对角线![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
由(1)得![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() .
.
∴![]() 的长为定值
的长为定值![]() .
.
(3)解:![]() .
.
理由:如图1,∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() .
.
由(1)知![]() ,
,
∴![]() .
.
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
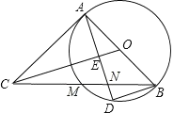
【题目】如图,AB是⊙O的直径,CA与⊙O相切于点A,且CA=BA.连接OC,过点A作AD⊥OC于点E,交⊙O于点D,连接DB.
(1)求证:△ACE≌△BAD;
(2)连接CB交⊙O于点M,交AD于点N.若AD=4,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
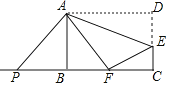
【题目】如图,矩形ABCD中,AB=12,AD=15,E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处,点P是线段CB延长线上的动点,连接PA,若△PAF是等腰三角形,则PB的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
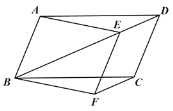
【题目】如图,在□ABCD中,点E是对角线BD上的一点,过点C作CF∥BD,且CF=DE,连接AE、BF、EF.
(1)求证:△ADE≌△BCF;
(2)若∠BFC-∠ABE=90°,判断四边形ABFE的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
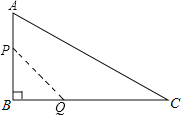
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快“智慧校园”建设,某市准备为试点学校采购一批![]() 、
、![]() 两种型号的一体机,经过市场调查发现,今年每套
两种型号的一体机,经过市场调查发现,今年每套![]() 型一体机的价格比每套
型一体机的价格比每套![]() 型一体机的价格多0.6万元,且用960万元恰好能购买500套
型一体机的价格多0.6万元,且用960万元恰好能购买500套![]() 型一体机和200套
型一体机和200套![]() 型一体机.
型一体机.
(1)求今年每套![]() 型、
型、![]() 型一体机的价格各是多少万元
型一体机的价格各是多少万元
(2)该市明年计划采购![]() 型、
型、![]() 型一体机1100套,考虑物价因素,预计明年每套
型一体机1100套,考虑物价因素,预计明年每套![]() 型一体机的价格比今年上涨25%,每套
型一体机的价格比今年上涨25%,每套![]() 型一体机的价格不变,若购买
型一体机的价格不变,若购买![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买![]() 型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该市明年至少需要投入多少万元才能完成采购计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.
(1)问:今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com