
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1 , 并直接写出C1点的坐标;
(2)以点B为位似中心,在网格中画出△A2BC2 , 使△A2BC2与△ABC位似,且位似比为2:1,并直接写出C2点的坐标及△A2BC2的面积.
【答案】
(1)
如图,△A1B1C1即为所求,C1(2,﹣2)
(2)
如图,
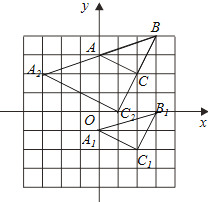
△A2BC2即为所求,C2(1,0),
△A2BC2的面积:
6×4﹣ ![]() ×2×6﹣
×2×6﹣ ![]() ×2×4﹣
×2×4﹣ ![]() ×2×4
×2×4
=24﹣6﹣4﹣4
=24﹣14
=10.
【解析】(1)根据网格结构,找出点A、B、C向下平移4个单位的对应点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出点C1的坐标;(2)延长BA到A2 , 使AA2=AB,延长BC到C2 , 使CC2=BC,然后连接A2C2即可,再根据平面直角坐标系写出C2点的坐标,利用△A2BC2所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
【考点精析】解答此题的关键在于理解作图-位似变换的相关知识,掌握对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】在数学中,有许多关系都是在不经意间被发现的.当然,没有敏锐的观察力是做不到的.数学家们往往是这样来研究问题的:特值探究–猜想归纳–逻辑证明–总结应用.下面我们也来像数学家们那样分四步找出这两个代数式的关系:对于代数式![]() 与
与![]() .
.
![]() 特值探究:
特值探究:
当![]() ,
,![]() 时,
时,![]() ________;
________;![]() ________
________
当![]() ,
,![]() 时,
时,![]() ________;
________;![]() ________
________
![]() 猜想归纳:
猜想归纳:
观察![]() 的结果,写出
的结果,写出![]() 与
与![]() 的关系:________.
的关系:________.
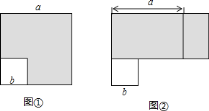
![]() 逻辑证明:如图,边长为
逻辑证明:如图,边长为![]() 的正方形纸片剪出一个边长为
的正方形纸片剪出一个边长为![]() 的小正方形之后,剩余部分(即阴影部分)又剪拼成一个矩形(不重叠无缝隙),请你说说是如何用这个图来得出
的小正方形之后,剩余部分(即阴影部分)又剪拼成一个矩形(不重叠无缝隙),请你说说是如何用这个图来得出![]() 中的关系?
中的关系?
![]() 总结应用:利用你发现的关系,求:
总结应用:利用你发现的关系,求:
①若![]() ,且
,且![]() ,则
,则![]() ________;
________;
②![]() 的值.(提示:你可能要用到公式
的值.(提示:你可能要用到公式![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的对称轴是直线x=2,顶点A的纵坐标为1,点B(4,0)在此抛物线上.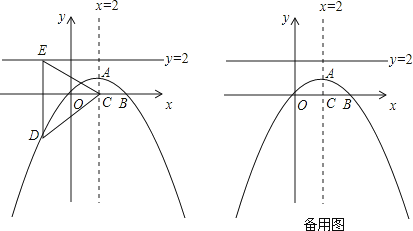
(1)求此抛物线的解析式;
(2)若此抛物线对称轴与x轴交点为C,点D(x,y)为抛物线上一动点,过点D作直线y=2的垂线,垂足为E.
①用含y的代数式表示CD2 , 并猜想CD2与DE2之间的数量关系,请给出证明;
②在此抛物线上是否存在点D,使∠EDC=120°?如果存在,请直接写出D点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD= ![]() ,④S△ODC=S四边形BEOF中,正确的有( )
,④S△ODC=S四边形BEOF中,正确的有( ) 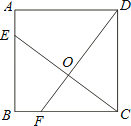
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() (2)
(2)![]()
(3)(-2![]() )-(+4.7)-(-0.4)+ (-3.3) (4)
)-(+4.7)-(-0.4)+ (-3.3) (4)![]()
(5)![]() (6)(
(6)(![]() -
-![]() +
+![]() )×(-36)
)×(-36)
(7)![]() (8)—
(8)—![]() (用简便方法计算)
(用简便方法计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险.半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同.
(1)问两队的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时刻,单位时间进出路口A,B,C的机动车辆数如图所示.图中x1,x2,x3分别表示该时段单位时间通过路段AB,BC,CA的机动车辆数(假设单位时间内在上述路段中同一路段上驶入与驶出的车辆数相等),则有( )

A. x1>x2>x3 B. x1>x3>x2 C. x2>x3>x1 D. x3>x2>x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深化理解:
新定义:对非负实数x “四舍五入”到个位的值记为![]() ,
,
即:当n为非负整数时,如果![]() ;
;
反之,当n为非负整数时,如果![]()
例如:<0> = <0.48> = 0,<0.64> = <1.49> = 1,<2> = 2,<3.5> = <4.12> = 4,……
试解决下列问题:
(1)填空:①![]() =________(
=________(![]() 为圆周率); ②如果
为圆周率); ②如果![]() 的取值范围为____________________.
的取值范围为____________________.
(2)若关于x的不等式组 的整数解恰有3个,求a的取值范围.
的整数解恰有3个,求a的取值范围.
(3)求满足![]() 的所有非负实数x的值.
的所有非负实数x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com