
【题目】已知![]() 是
是![]() 的直径,弦
的直径,弦![]() 与
与![]() 相交,
相交,![]() .
.
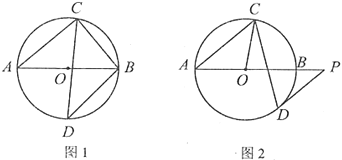
(1)如图,若![]() 为弧
为弧![]() 的中点,求
的中点,求![]() 和
和![]() 的度数;
的度数;
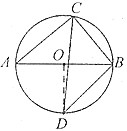
(2)如图,若D为弧![]() 上一点,过点
上一点,过点![]() 作
作![]() 的切线,与
的切线,与![]() 的延长线交于点
的延长线交于点![]() ,若DP//AC,求∠OCD的度数.
,若DP//AC,求∠OCD的度数.
【答案】(1)∠ABC=50°,![]() ;(2)∠OCD=25°.
;(2)∠OCD=25°.
【解析】
(1)由AB为直径可得∠ACB=90°,进而可求出∠ABC的度数;根据D为![]() 的中点可得∠BOD=90°,由等腰三角形的性质即可求出∠ABD的度数;(2)连接OD,由切线性质可得
的中点可得∠BOD=90°,由等腰三角形的性质即可求出∠ABD的度数;(2)连接OD,由切线性质可得![]() ,根据平行线的性质可得∠P=∠CAB=40°,根据外角性质可求出∠AOD的度数,根据圆周角定理可得∠ACD的度数,由等腰三角形的性质可得
,根据平行线的性质可得∠P=∠CAB=40°,根据外角性质可求出∠AOD的度数,根据圆周角定理可得∠ACD的度数,由等腰三角形的性质可得![]() ,根据
,根据![]() 即可得答案.
即可得答案.
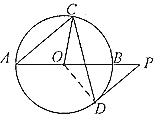
(1)如图1,连接![]() ,
,
∵AB为直径,
∴∠ACB=90°,
∴∠ABC=90°-∠BAC=50°,
∵![]() 为弧
为弧![]() 的中点,
的中点,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)如图2,连接![]() ,
,
∵![]() 切
切![]() 于点
于点![]() ,
,
∴![]() ,即
,即![]() .
.
由![]() ,又
,又![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 的一个外角,
的一个外角,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数 | 30 | 75 | 130 | 210 | 480 | 856 | 1250 | 2300 |
发芽数 | 28 | 72 | 125 | 200 | 457 | 814 | 1187 | 2185 |
发芽频率 | 0.9333 | 0.9600 | 0.9615 | 0.9524 | 0.9521 | 0.9509 | 0.9496 | 0.9500 |
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是_____(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,![]() .在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角
.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角![]() 为
为![]() (点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)
(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)![]() ,那么建筑物AB的高度约为( )
,那么建筑物AB的高度约为( )
(参考数据![]() ,
,![]() ,
,![]() )
)
A.65.8米B.71.8米C.73.8米D.119.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,BE平分
中,BE平分![]() 交AD于点E.
交AD于点E.

(1)如图1,若![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(2)如图2,过点A作![]() ,交DC的延长线于点F,分别交BE,BC于点G,H,且
,交DC的延长线于点F,分别交BE,BC于点G,H,且![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.
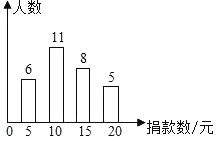
(1)本次调查的样本容量是________,这组数据的众数为________元;
(2)求这组数据的平均数;
(3)该校共有![]() 学生参与捐款,请你估计该校学生的捐款总数.
学生参与捐款,请你估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
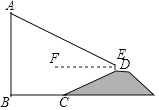
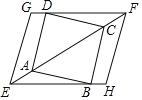
【题目】如图,在正方形ABCD中,分别过顶点B,D作![]() 交对角线AC所在直线于E,F点,并分别延长EB,FD到点H,G,使
交对角线AC所在直线于E,F点,并分别延长EB,FD到点H,G,使![]() ,连接EG,FH.
,连接EG,FH.
(1)求证:四边形EHFG是平行四边形;
(2)已知:![]() ,
,![]() ,
,![]() ,求四边形EHFG的周长.
,求四边形EHFG的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
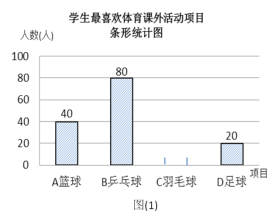
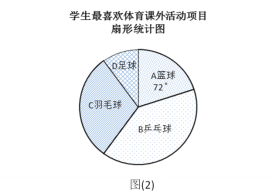
【题目】某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A篮球;B乒乓球;C羽毛球;D足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有__________人;
(2)请你将条形统计图(1)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点P是直线AC上一点,将△ADP沿DP所在的直线翻折后,点A落在A1处,若A1D⊥AC,则点P与点A之间的距离为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com