
【题目】如图,将一块直角三角形纸板的直角顶点放在C(1,![]() )处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
)处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+![]() 与双曲线y=
与双曲线y=![]() (m>0)的交点.
(m>0)的交点.
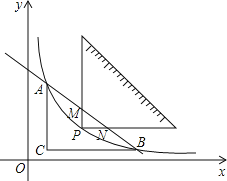
(1)求m和k的值;
(2)设双曲线y=![]() (m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=
(m>0)在A,B之间的部分为L,让一把三角尺的直角顶点P在L上滑动,两直角边始终与坐标轴平行,且与线段AB交于M,N两点,请探究是否存在点P使得MN=![]() AB,写出你的探究过程和结论.
AB,写出你的探究过程和结论.
【答案】(1)k=﹣![]() ;m=4 ;(2)不存在,理由见解析.
;m=4 ;(2)不存在,理由见解析.
【解析】
(1)由题意易知点A横坐标为1,代入y=![]() ,可用含m的代数式表示它的纵坐标;同理可表示点B坐标,再代入方程组
,可用含m的代数式表示它的纵坐标;同理可表示点B坐标,再代入方程组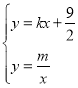 即可求m和k的值;
即可求m和k的值;
(2)用反证法证明.假设存在,运用一元二次方程判别式即可解出.
解:(1)∵A,B在双曲线y=![]() (m>0)上,AC∥y轴,BC∥x轴,
(m>0)上,AC∥y轴,BC∥x轴,
∴A,B的坐标分别(1,m),(2m,![]() )
)
又点A,B在直线y=kx+![]() 上,
上,
∴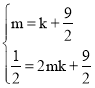
解得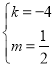 或
或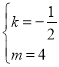
当k=﹣4且m=![]() 时,点A,B的坐标都是(1,
时,点A,B的坐标都是(1,![]() ),不合题意,应舍去;
),不合题意,应舍去;
当k=﹣![]() 且m=4时,点A,B的坐标分别为(1,4),(8,
且m=4时,点A,B的坐标分别为(1,4),(8,![]() ,符合题意.
,符合题意.
∴k=﹣![]() ,m=4.
,m=4.
(2)假设存在点P使得MN=![]() AB.
AB.
∵AC∥y轴,MP∥y轴,
∴AC∥MP,
∴∠PMN=∠CAB,
∴Rt△ACB∽Rt△MPN,
∴![]() ,
,
设点P坐标为P(x,![]() )(1<x<8),
)(1<x<8),
∴M点坐标为M(x,﹣![]() x+
x+![]() ),
),
∴MP=﹣![]() x+
x+![]() -
-![]() .
.
又∵AC=4﹣![]() ,
,
∴![]() ,即2x2﹣11x+16=0(※)
,即2x2﹣11x+16=0(※)
∵△=(﹣11)2﹣4×2×16=﹣7<0.
∴方程(※)无实数根.
∴不存在点P使得MN=![]() AB.
AB.


科目:初中数学 来源: 题型:
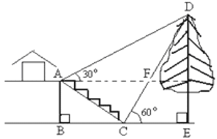
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船往返于一条河的两码头之间,如果船本身在静水中的速度是固定的,那么,当这条河的水流速度增大时,船往返一次所用的时间将( )
A.增多B.减少C.不变D.增多、减少都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
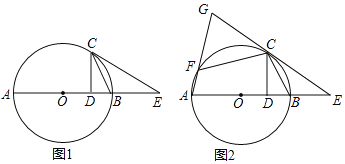
【题目】如图1,AB为⊙O的直径,C为⊙O上一点,连接CB,过C作CD⊥AB于点D,过点C作∠BCE,使∠BCE=∠BCD,其中CE交AB的延长线于点E.
(1)求证:CE是⊙O的切线.
(2)如图2,点F在⊙O上,且满足∠FCE=2∠ABC,连接AF井延长交EC的延长线于点G.
①试探究线段CF与CD之间满足的数量关系;
②若CD=4,BD=2,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
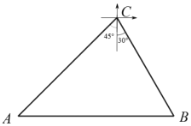
【题目】如图,正在海岛![]() 西南方向20海里作业的海监船
西南方向20海里作业的海监船![]() ,收到位于其正东方向渔船
,收到位于其正东方向渔船![]() 发出的遇险求救信号,已知渔船
发出的遇险求救信号,已知渔船![]() 位于海岛
位于海岛![]() 的南偏东
的南偏东![]() 方向,海岛
方向,海岛![]() 周围13海里内都有暗礁.(参考数据
周围13海里内都有暗礁.(参考数据![]() ,
,![]() )
)
(1)如果海监船![]() 沿正东方向前去救援是否有触礁的危险?
沿正东方向前去救援是否有触礁的危险?
(2)求海监船![]() 与渔船
与渔船![]() 的距离.(结果精确到0.1海里)
的距离.(结果精确到0.1海里)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=![]() x2+bx+c经过点A(-1,0),B(5,0).
x2+bx+c经过点A(-1,0),B(5,0).

(1)求抛物线的解析式并写出顶点M的坐标;
(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下统计图:

(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为___________度
(2)请补充完整下面的成绩统计分析表:
平均数 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 |
|
乙组 | 1.36 |
|
(3)你认为那组成绩较好?从以上信息中写出两条支持你的选择
(4)从甲、乙两组得9分的学生中抽取两人参加市级比赛,求这两人来自不同组的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com