
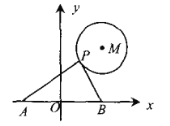
【题目】如图,![]() 的半径为2,圆心
的半径为2,圆心![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 上的任意一点,
上的任意一点,![]() ,且
,且![]() 、
、![]() 与
与![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,若点
两点,若点![]() 、点
、点![]() 关于原点
关于原点![]() 对称,则
对称,则![]() 的最大值为( )
的最大值为( )
A.7B.14C.6D.15
科目:初中数学 来源: 题型:
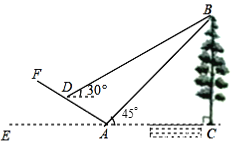
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1︰2.则小明从点A走到点D的过程中,他上升的高度为____米;大树BC的高度为____米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCO的顶点B、C在第二象限,点A(﹣3,0),反比例函数y=![]() (k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )
(k<0)图象经过点C和AB边的中点D,若∠B=α,则k的值为( )

A. ﹣4tanαB. ﹣2sinαC. ﹣4cosαD. ﹣2tan
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期猪肉价格不断走高,引起市民与政府的高度关注,当市场猪肉的平均价格达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从今年年初至5月20日,猪肉价格不断走高,5月20日比年初价格上涨了60%,某市民在今年5月20日购买2.5千克猪肉至少要花100元钱,那么今年年初猪肉的最低价格为每千克多少元?
(2)5月20日猪肉价格为每千克40元,5月21日,某市决定投入储备猪肉,并规定其销售价格在5月20日每千克40元的基础上下调a%出售,某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为40元的情况下,该天的两种猪肉总销量比5月20日增加了a%,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比5月20日提高了
,两种猪肉销售的总金额比5月20日提高了![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
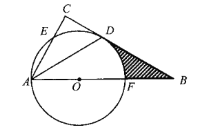
【题目】如图,在![]() 中,
中,![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 为半径的圆恰好经过点
为半径的圆恰好经过点![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]()
(1)试判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)若![]() ,
,![]() ,求阴影部分的面积(结果保留
,求阴影部分的面积(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P1(﹣1,y1),P2(2,y2),P3(5,y3)均在二次函数y=﹣x2+2x+c的图象上,则y1,y2,y3的大小关系是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象经过点(2,-5),顶点坐标为(-1,4),直线l的解析式为y=2x+m.
(1)求抛物线的解析式;
(2)若抛物线与直线l有两个公共点,求![]() 的取值范围;
的取值范围;
(3)若直线l与抛物线只有一个公共点P,求点P的坐标;
(4)设抛物线与![]() 轴的交点分别为A、B,求在(3)的条件下△PAB的面积.
轴的交点分别为A、B,求在(3)的条件下△PAB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com