
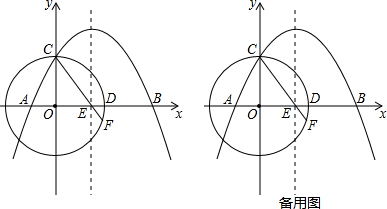
���� ��1���������⣬���ȸ���Բ��y��Ľ��������C�����꣬��A��B��C��������룬�ô���ϵ������������ߵĽ���ʽ��
��2���������������Ƽ����������Ĵ𰸣�
��3����ͼ������P��x��Ĵ��ߣ�����ΪH�����ý�ֱ�������ε�֪ʶ�����������Ĵ𰸣�
��� �⣺��1������OΪԲ�ģ��뾶Ϊ1�ġ�Oǡ�þ�����C��
���C��0��1����
��A����0����B��2��0����C��0��1���������y=ax2+bx+c�ã�
$\left\{\begin{array}{l}{c=1}\\{\frac{1}{4}a-\frac{1}{2}b+c=0}\\{4a+2b+c=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-1}\\{b=1.5}\\{c=1}\end{array}\right.$��
�������ߵĺ�������ʽΪy=-x2+1.5x+1��
��2��x=$-\frac{b}{2a}$=$-\frac{1.5}{-2}$=0.75��
��Rt��COE��OC=1��OE=0.75��
��CE=$\sqrt{{1}^{2}+0.7{5}^{2}}$=$\frac{5}{4}$��
���O��y��ĸ����ύ��ΪG������FG��
���CFG=��COE=90�㣬��OCE=��FCG��
���CEO�ס�CGF��
��$\frac{CE}{CG}$=$\frac{CO}{CF}$��
���CF=$\frac{CO•CG}{CE}$=$\frac{1��2}{\frac{5}{4}}$=$\frac{8}{5}$��
��EF=$\frac{8}{5}$-$\frac{5}{4}$=$\frac{7}{20}$�� ��3����ͼ������P��x��Ĵ��ߣ�����ΪH����BH=2-m��PH=|n|��
��3����ͼ������P��x��Ĵ��ߣ�����ΪH����BH=2-m��PH=|n|��
��ֱ�ǡ�PHB�У�tanB=|$\frac{n}{2-m}$|��
��ΪtanB���B�����������
����|$\frac{n}{2-m}$|��ֵ���ʱ����B��ֵ���
��ʱ��ֱ�����O���У��е�Ϊ��P��
����OP��
��ֱ�ǡ�0PB�У�sinB=$\frac{OP}{AB}$=$\frac{1}{2}$��
���ԡ�B=30�㣬
��ֱ�ǡ�0MB�У���OM=$\frac{{2\sqrt{3}}}{3}$��
��M��0��$\frac{2\sqrt{3}}{3}$����
��ֱ��BP�Ľ���ʽΪ��y=kx+b����$\left\{\begin{array}{l}{b=\frac{2\sqrt{3}}{3}}\\{2k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=\frac{2\sqrt{3}}{3}}\end{array}\right.$��
��ֱ��BP��Ӧ�ĺ�������ʽΪ$y=-\frac{{\sqrt{3}}}{3}x+\frac{{2\sqrt{3}}}{3}$��
ͬ������õ���P��x���·�ʱֱ��BP��Ӧ�ĺ�������ʽΪ$y=\frac{{\sqrt{3}}}{3}x-\frac{{2\sqrt{3}}}{3}$��
���� ������Ҫ�����˶��κ���֪ʶ���ۺ����ã��Լ�����ϵ���������Ľ���ʽ�����������ε�֪ʶ����һ�����κ�����һ�κ������Լ�����֪ʶ���ϵ���Ŀ���ѶȱȽϴ�Ҫע���ܽᣮ


 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
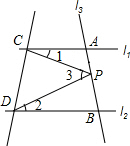 ��ͼ����ֱ֪��l1��l2����l3��l1��l2�ֱ���A��B���㣬��P��ֱ��AB�ϣ���PC��l1���еĽ�Ϊ��1��PD��l2���еĽ�Ϊ��2����CPDΪ��3��
��ͼ����ֱ֪��l1��l2����l3��l1��l2�ֱ���A��B���㣬��P��ֱ��AB�ϣ���PC��l1���еĽ�Ϊ��1��PD��l2���еĽ�Ϊ��2����CPDΪ��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
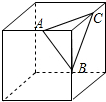 ��ͼ����A��B��C��������������������е㣬��A��B��C�������ڵ�ƽ�潫���������
��ͼ����A��B��C��������������������е㣬��A��B��C�������ڵ�ƽ�潫���������| A�� | 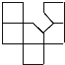 | B�� | 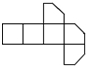 | C�� | 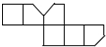 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
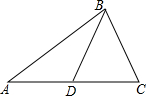 ��ͼ��BD�ǡ�ABC�����ߣ�AB��BC��AD=2��AB=6��BC=3�����ABD�������4.5��
��ͼ��BD�ǡ�ABC�����ߣ�AB��BC��AD=2��AB=6��BC=3�����ABD�������4.5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 4 | C�� | 7 | D�� | 7��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
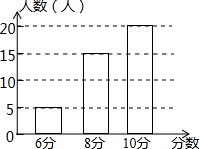 ��һ���������ϣ�������ʦ�Ծ��꼶һ���40��ͬѧ������������Զ��Ŀ�IJ��ԣ��������÷�������Ӧ��������ͼ��ʾ����β��Ե�ƽ����Ϊ8.75�֣�
��һ���������ϣ�������ʦ�Ծ��꼶һ���40��ͬѧ������������Զ��Ŀ�IJ��ԣ��������÷�������Ӧ��������ͼ��ʾ����β��Ե�ƽ����Ϊ8.75�֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 2 | D�� | -2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com