
【题目】把下面的推理过程补充完整,并在括号内注明理由.如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,试说明:∠C=∠F;AC∥DF.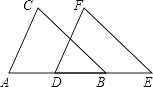
解:∵AD=BE(已知)
∴AD+DB=DB+BE()
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠()
又∵BC=EF(已知)
∴△ABC≌△DEF()
∴∠C=∠F,∠A=∠FDE()
∴AC∥DF()
科目:初中数学 来源: 题型:
【题目】今年海南西瓜收成良好,小华家也喜获丰收,小华家今年种植“黑美人”西瓜5亩,“无籽”西瓜20亩,共收70000千克,按市场价“黑美人”每千克2.4元,“无籽”西瓜每千克4元出售,收入264000元.
(1)小华家今年种植的“黑美人”西瓜和“无籽”西瓜亩产各多少千克?
(2)如果知道种植1亩“黑美人”西瓜的成本为3000元,1亩“无籽”西瓜的成本为4000元,小华家今年种植西瓜共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表达式为![]() ,孔明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a还是b表示多边形内部的整点个数,请你选择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部的整点个数的字母是 ,并运用这个公式求得图2中多边形的面积是 .
,孔明只记得公式中的S表示多边形的面积,a和b中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a还是b表示多边形内部的整点个数,请你选择一些特殊的多边形(如图1)进行验证,得到公式中表示多边形内部的整点个数的字母是 ,并运用这个公式求得图2中多边形的面积是 .
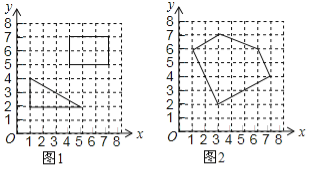
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 过点P画线段AB的垂线
B. P是直线外一点,Q是直线上一点,连接PQ,PQ⊥AB
C. 过一点有且只有一条直线平行于已知直线
D. 线段AB就是表示A,B两点间的距离
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,BC=8cm,AC=6cm,在射线BC上一动点D,从点B出发,以2厘米每秒的速度匀速运动,若点D运动t秒时,以A、D、B为顶点的三角形恰为等腰三角形,则所用时间t为秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m= .
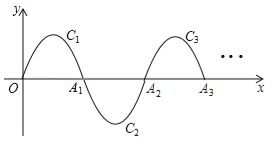
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一种“二十四点”的游戏,其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3,4,可作如下运算:(1+2+3)×4=24(上述运算与4×(1+2+3)视为相同方法的运算)现有四个有理数3,4, ![]() ,10,运用上述规则写出三种不同方法的运算式,可以使用括号,使其结果等于24.运算式分别为:
,10,运用上述规则写出三种不同方法的运算式,可以使用括号,使其结果等于24.运算式分别为:
(1);
(2);
(3)﹒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com