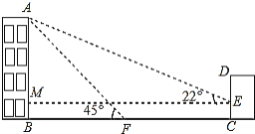
【题目】如图，某办公楼AB的右边有一建筑物CD，在建设物CD离地面2米高的点E处观测办公楼顶A点，测得的仰角
=
，在离建设物CD 25米远的F点观测办公楼顶A点，测得的仰角
=
（B，F，C在一条直线上）．
（1）求办公楼AB的高度；
（2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．（参考数据：
）
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，已知抛物线
经过点A(3，1)与点B(0，4)．
(1)求该抛物线的解析式及顶点坐标；
(2)在第三象限内的抛物线上有一点P，使得PA⊥AB，求点P的坐标；
(3)若点C(
，
)在该抛物线上，当
≤≤3时，1≤≤5，请确定的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB．
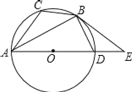
⑴求证：BE是⊙O的切线；
⑵若BC=
，AC=5，求圆的直径AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形
中，
，
，点
、
分别在边
和
上，沿
折叠四边形，使点
、
分别落在
、
处，得四边形
，点在
上，过点作
于点
，连接
，则下列结论：①
；②
；
③
；④若点是
的中点，则
，其中，正确结论的序号是_______.（把所有正确结论的序号都在填在横线上）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形 ABCD 中，AB=8，BC=6，将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AEFG，AE，FG 分别交射线CD 于点 PH，连结 AH，若 P 是 CH 的中点，则△APH 的周长为（ ）
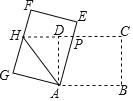
A. 15 B. 18 C. 20 D. 24
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线
与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB．则△PAB面积的最大值是（ ）
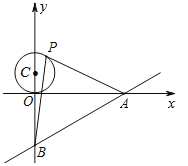
A.8B.12C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知四边形
和四边形
都是正方形，且
．
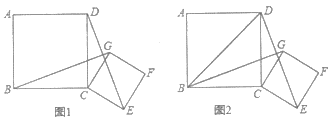
（1）如图1，连接
、
．求证：
；
（2）如图2，将正方形绕着点
旋转到某一位置时恰好使得
，
．求
的度数；
（3）在（2）的条件下，当正方形的边长为
时，请直接写出正方形的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在直角坐标系中，已知抛物线
(a＜0)与x轴交于A、B两点(点A在点B左侧)，与y轴负半轴交于点C，顶点为D，已知
：S四边形ACBD=1：4．
（1）求点D的坐标(用仅含c的代数式表示)；
（2）若tan∠ACB=
，求抛物线的解析式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
