
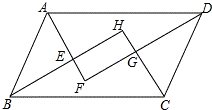
 如图,平行四边形的四个内角的平分线分别相交于点E、F、G、H,四边形EFGH是怎么样的特殊四边形?证明你的结论.
如图,平行四边形的四个内角的平分线分别相交于点E、F、G、H,四边形EFGH是怎么样的特殊四边形?证明你的结论.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
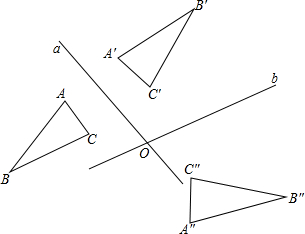 你还记得某个图形关于两平行直线依次作出某一图形的轴对称图形,其最后的图形可以由原图形经过一次平移而得到.
你还记得某个图形关于两平行直线依次作出某一图形的轴对称图形,其最后的图形可以由原图形经过一次平移而得到.查看答案和解析>>
科目:初中数学 来源: 题型:
 小明把手臂水平向前伸直,手持小尺,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处恰好能看到铁塔的顶部B和底部A.设小明的手臂长L=50cm,小尺长a=20cm,点D到铁塔底部的距离AD=40m,求铁塔的高度.
小明把手臂水平向前伸直,手持小尺,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处恰好能看到铁塔的顶部B和底部A.设小明的手臂长L=50cm,小尺长a=20cm,点D到铁塔底部的距离AD=40m,求铁塔的高度.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,以BC为边在矩形ABCD内作等边三角形OBC,连接DO并延长交AB于点E,连接EC,过点C作CF∥DE,交AB的延长线于点F.
已知:如图,以BC为边在矩形ABCD内作等边三角形OBC,连接DO并延长交AB于点E,连接EC,过点C作CF∥DE,交AB的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com