
【题目】已知,点E、F分别在直线AB,CD上,点P在AB、CD之间,连结EP、FP,如图1,过FP上的点G作GH∥EP,交CD于点H,且∠1=∠2.
(1)求证:AB∥CD;
(2)如图2,将射线FC沿FP折叠,交PE于点J,若JK平分∠EJF,且JK∥AB,则∠BEP与∠EPF之间有何数量关系,并证明你的结论;
(3)如图3,将射线FC沿FP折叠,将射线EA沿EP折叠,折叠后的两射线交于点M,当EM⊥FM时,求∠EPF的度数.

【答案】(1)证明见解析;(2)∠BEP+![]() ∠EPF=180.证明见解析;(3)∠EPF=135
∠EPF=180.证明见解析;(3)∠EPF=135
【解析】试题分析:(1)延长FP交AB于点Q,根据平行线性质可得∠2=∠3,再由∠1=∠2可得∠1=∠3,即可证明结论;(2)过点P作PM∥CD,即可证得JK∥AB∥CD∥PM,根据平行线的性质解答即可;(3)作PG∥AB,MH∥AB,则PG∥MH∥AB∥CD,根据平行线的性质进行分析解答即可.
试题解析:
延长EP交CD于点Q
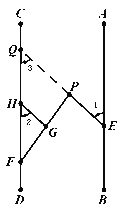
∵GH∥PE,
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴AB∥CD.
(2)过点P作PM∥CD,又AB∥CD,∴PM∥AB.

∴∠FPM=∠1,∠EPM=∠2,
∴∠FPE=∠FPM+∠EPM=∠1+∠2.
又∵JK∥AB∥CD,
同理可证:∠FJE=∠CFJ+∠2.
又∵∠FJK=∠CFJ=2∠1=∠3=∠2,
∵∠BEP+∠3=180,
∴∠BEP+2∠1=180,
∴∠BEP+2(∠EPF-∠2)=180,
∴∠BEP+2∠EPF-2∠2=180,
∴∠BEP+2∠EPF-2(180-∠BEP)=180.
即:![]()
(3)作PG∥AB,MH∥AB,则PG∥MH∥AB∥CD.
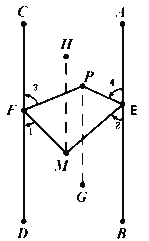
∵FM⊥EM,∴∠EMF=90
易证:∠1+∠2=∠EMF=90,∠EPF=∠3+∠4,
又∵∠3=∠PFM,∠4=∠PEM,
∴∠1=180-2∠3,∠2=180-2∠4.
∴180-2∠3+180-2∠4=90,
∴2∠3+2∠4=270.
∴∠3+∠4=135,
∴∠EPF=135


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】根据题意计算与解答
(1)计算(x﹣y)2﹣(x﹣2y)(x+y)
(2)若关于x,y的二元一次方程组 ![]() 的解满足x+y>﹣
的解满足x+y>﹣ ![]() ,求出满足条件的m的所有正整数值.
,求出满足条件的m的所有正整数值.
(3)若关于x的方程 ![]() +
+ ![]() =3的解为正数,求m的取值范围.
=3的解为正数,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是马小哈同学做的一道题:
解方程:![]()
解:①去分母,得 4(2x﹣1)=1﹣3(x+2)
②去括号,得 8x﹣4=1﹣3x﹣6
③移项,得8x+3x=1﹣6+4
④合并同类项,得 11x=﹣1
⑤系数化为1,得![]()
(1)上面的解题过程中最早出现错误的步骤是(填代号) ;
(2)请在本题右边正确的解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC,任取一点O,连AO,BO,CO,并取它们的中点D,E,F,得△DEF,则下列说法正确的个数是( ) ①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.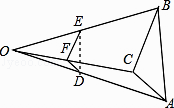
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先计算:
![]() =________,
=________,![]() =________,
=________,![]() =________,
=________,
![]() =________,
=________,![]() =0.
=0.
根据计算结果,回答:
(1) ![]() 一定等于a吗?如果不是,那么
一定等于a吗?如果不是,那么![]() =________;
=________;
(2)利用你总结的规律,计算:
①若x<2,则![]() =________;
=________;
②![]() =________.
=________.
(3)若a,b,c为三角形的三边长,化简:
![]() +
+![]() +
+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.
(1)请在图中标出景点C的位置;
(2)小明想从景点B开始游玩,途经景点A,最后到达景点C,求小明一家最短的行走路程(参考数据:![]() ≈6,结果保留整数).
≈6,结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
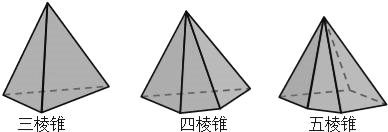
【题目】设棱锥的顶点数为V,面数为F,棱数为E.
(1)观察与发现:三棱锥中,V3= ,F3= ,E3= ;
五棱锥中,V5= ,F5= ,E5= ;
(2)猜想:①十棱锥中,V10= ,F10= ,E10= ;
②n棱锥中,Vn= ,Fn= ,En= ;(用含有n的式子表示)
(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系: ;
②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:E= ;
(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间是否也存在某种等量关系?若存在,试写出相应的等式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是平面上的两定点,在平面上找一点C,使△ABC为等腰直角三角形,且点C为直角顶点,这样的点C有几个?请用尺规作图确定点C的位置,保留作图迹并说明理由
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com