【题目】如图，将半径为6的圆形纸片，分别沿AB、BC折叠，若弧AB和弧BC折后都经过圆心O，则阴影部分的面积是（结果保留π）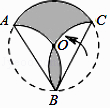 
【答案】12π
【解析】解：作OD⊥AB于点D，连接AO，BO，CO，如图所示：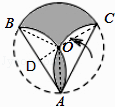 
∵OD= 
AO
∴∠OAD=30°，
∴∠AOB=2∠AOD=120°，
同理∠BOC=120°，
∴∠AOC=120°，
∴阴影部分的面积=S扇形BOC= 
×⊙O面积= ×π×62=12π；
所以答案是：12π．
【考点精析】根据题目的已知条件，利用扇形面积计算公式和翻折变换（折叠问题）的相关知识可以得到问题的答案，需要掌握在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
科目：初中数学 来源： 题型：
【题目】在ABCD中，AB=10，BC=14，E，F分别为边BC，AD上的点，若四边形AECF为正方形，则AE的长为（ ）
A.7
B.4或10
C.5或9
D.6或8
查看答案和解析>>
科目：初中数学 来源： 题型：
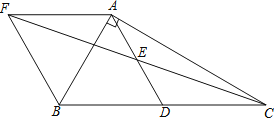
【题目】如图，在△ABC中，∠BAC=90°，AB=4，tan∠ACB=
，点D、E分别是BC、AD的中点，AF∥BC交CE的延长线于点F，则四边形AFBD的面积为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A′处；
（1）求证：B′E=BF；
（2）设AE=a，AB=b，BF=C，试猜想a，b，c之间的一种关系，并给予证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，数轴上点 A、B 到表示-2 的点的距离都为 6，P 为线段 AB 上任一点，C，D 两点分别从 P，B 同时向 A 点移动，且 C 点运动速度为每秒 2 个单位长度，D 点运动速度 为每秒 3 个单位长度，运动时间为 t 秒.
（1）A 点表示数为 ，B 点表示的数为 ，AB= .
（2）若 P 点表示的数是 0，
①运动 1 秒后，求 CD 的长度；
②当 D 在 BP 上运动时，求线段 AC、CD 之间的数量关系式.
（3）若 t=2 秒时，CD=1，请直接写出 P 点表示的数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市水果批发部门欲将A市的一批水果运往本市销售，有火车和汽车两种运输方式，运输过程中的损耗均为200元／时。其它主要参考数据如下：
运输工具 | 途中平均速度（千米／时） | 运费（元／千米） | 装卸费用（元） |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果汽车的总支出费用比火车费用多1100元，你知道本市与A市之间的路程是多少千米吗？请你列方程解答．
(2)如果A市与某市之间的距离为S千米，且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时，你若是某市水果批发部门的经理，要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，点E、F分别在直线AB，CD上，点P在AB、CD之间，连结EP、FP，如图1，过FP上的点G作GH∥EP，交CD于点H，且∠1=∠2．
（1）求证：AB∥CD；
（2）如图2，将射线FC沿FP折叠，交PE于点J，若JK平分∠EJF，且JK∥AB，则∠BEP与∠EPF之间有何数量关系，并证明你的结论；
（3）如图3，将射线FC沿FP折叠，将射线EA沿EP折叠，折叠后的两射线交于点M，当EM⊥FM时，求∠EPF的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
